WIKI de Bertrand VANDEPORTAELE

La démarche de développement est composée de deux grandes étapes. La première étape consiste en l'implémentation d'un filtre logiciel qui permet de vérifier si le filtre possède bien les propriétés temporelles et/ou fréquentielles souhaitées. Cette étape réalisée lors des séances de TNS est composée de la façon suivante:

1. définition du filtre (coefficients stockés dans des tableaux, initialisation d'un sFiltre avec initFiltre() )
2. définition des signaux (création de tableaux pour l'impulsion, l'échelon, sinus…) pour une durée fixée
3. calcul de la réponse du filtre pour tous les échantillons du signal d'entrée (avec calculReponseFiltre() )
4. affichage des signaux d'entrée et de sortie
5. affichage éventuel de la fonction de transfert
6. fin du programme

La seconde étape consiste en la réalisation concrète du filtre en tenant compte du matériel utilisé, le programme devant assurer les tâches suivantes:

1. définition du filtre
2. acquisition d'un échantillon ek en effectuant une conversion analogique→numérique
3. calcul de sk en appliquant l'équation de récurrence sur cet échantillon
4. restituer sk en effectuant une conversion numérique→analogique
5. recommencer indéfiniment en 2. jusqu'à l'arrêt du système !

Cette seconde étape est l'objectif des TP du module Architecture pour le TNS. Le filtre sera réalisé sur une carte Nucléo intégrant un microcontrôleur de la famille STM32 de STMicroelectronics.

POUR LA PREMIERE SEANCE UNIQUEMENT!, pour récupérez le fichier projet la première fois, ouvrir une console (alt+F2 et taper lxterm) puis copier coller (sélectionner le code qui suit puis clic sur le bouton central de la souris dans le terminal) :

echo "commence ici"
cd ~/
rm -f TP_ARCHI_TNS_ETU.zip
wget https://bvdp.inetdoc.net/files/iut/tp_tns/TP_ARCHI_TNS_ETU.zip
unzip TP_ARCHI_TNS_ETU.zip
rm -f TP_ARCHI_TNS_ETU.zip
cd TP_ARCHI_TNS_ETU
git init
git add *
git commit -m'initial version'
qtcreator TP_ARCHI_TNS.pro &
echo "C est bon !"

à l'ouverture de qtcreator, cliquer sur “Configurer le projet”

1. filtre.h et filtre.cpp: contient la classe Filtre permettant de réaliser le filtrage “en ligne”. Les méthodes de cette classe devront être implémentées par vous. Ces fichiers seront les seuls utilisés sur le microcontroleur et c'est principalement le fichier filtre.cpp que vous devrez compléter.
2. filtretrace.h et filtretrace.cpp: contient une classe dérivée de Filtre dans laquelle nous avons ajouté diverses méthodes pour le tracé et la comparaison des réponses (avec une méthode de filtrage “hors ligne”). Ces fichiers ne seront pas utilisés sur le microcontroleur et vous n'aurez pas à le modifier.
3. tparchi1.cpp: contient la fonction de test void code_tparchi1(void). Elle permet de créer des échantillons pour les signaux d'entrée et de tracer les réponses impulsionnelle, indicielle et le module de la réponse fréquentielle en invoquant les méthodes implémentées dans Filtre et FiltreTrace. Vous aurez à modifier ce fichier.
4. prototype_tp.h: contient les prototypes des fonctions de test
5. main.cpp: contient le programme principal, qui appelle la fonction de test.
6. mainwindow.h et mainwindow.cpp: contiennent la classe qui permet l'affichage de la fenêtre principale de l'application
7. qcustomplot.h et qcustomplot.cpp: contiennent les classes qui permettent l'affichage de tracé graphique

Afin de pouvoir facilement changer certains types et de pouvoir répercuter les changements partout dans le code, nous avons définis 2 types personnalisés pour:

1. le stockage des coefficients du échantillons en entrée/sortie/résultats intermédiaires: type echantillon_t.
2. le stockage des coefficients du filtre: type coefficient_t.

Pour le projet QT, ces définitions seront les suivantes et vous utiliserez ces types au lieu de double dans tout votre code:

//définition du type utilisé pour les échantillons et les coefficients sous QT
typedef double echantillon_t;
typedef double coefficient_t;

Polycopié du cours de P.O.O. : cours_POO_intro9_2019.pdf

Le code et les données pour le filtre sont rangés dans une classe Filtre. Les membres de la classe Filtre sont déclarés dans le fichier filtre.h et l'implémentation des méthodes est réalisée dans le fichier filtre.cpp.

Les attributs de Filtre sont déclarés en protected afin de réaliser l'encapsulation et ne seront donc accessibles que depuis les méthodes de Filtre (et dans la classe dérivée FiltreTrace).

Les méthodes de Filtre sont déclarées en public afin de pouvoir les invoquer depuis l'extérieur de la classe Filtre.

Pour vous, les attributs de la classe Filtre seront utilisables comme des variables globales accessibles dans les différentes méthodes de filtre.

La définition de la classe Filtre est donnée ici:

class Filtre
{
public:
    Filtre(int nbInitB, coefficient_t *pBInit, int nbInitA, coefficient_t *pAInit,int nbMemoireVkInit=0, echantillon_t *memoireVkInit=NULL, int offsetEntreeInit=0, int offsetSortieInit=0, int valeurSortieMaxInit=10000, int valeurSortieMinInit=-10000);
    void ResetMemoireVk();
    echantillon_t TraiteUnEchantillon(echantillon_t ek);
    void setADCDAC(    int offsetEntreeInit, int offsetSortieInit, int valeurSortieMaxInit, int valeurSortieMinInit){
        offsetEntree=offsetEntreeInit;
        offsetSortie=offsetSortieInit;
        valeurSortieMax=valeurSortieMaxInit;
        valeurSortieMin=valeurSortieMinInit;
    }
protected:                    //attributs accessibles dans les classes dérivées
    int nbCoeffB;             //nombre de coefficients du numérateur de la fonction de transfert du filtre
    coefficient_t * pCoeffB;  //Coefficients du numérateur de la fonction de transfert du filtre
    int nbCoeffA;             //nombre de coefficients du dénominateur de la fonction de transfert du filtre
    coefficient_t * pCoeffA;  //Coefficients du dénominateur de la fonction de transfert du filtre
                              //le premier élément est a1
                              //le tableau est de taille 1 pour un RIF
    int nbMemoireVk;          //nombre de cases du buffer circulaire pour stocker les valeurs de vk
    echantillon_t * memoireVk;//buffer circulaire pour stocker les valeurs de vk
    int indice_ecr;           //indice d'écriture dans le buffer rotatif memoireVk
                              //paramètres ADC/DAC
    int offsetEntree;         //offset retranché aux échantillons en entrée
    int offsetSortie;         //offset ajouté aux échantillons en sortie
    int valeurSortieMax;      //valeur maximale pour les échantillons de sortie avant ajout de offsetSortie
    int valeurSortieMin;      //valeur minimale pour les échantillons de sortie avant ajout de offsetSortie
    };

La classe FiltreTrace est définie comme classe fille de la classe Filtre. Elle peut donc faire tout ce que Filtre peut faire mais contient également du code de test, d'affichage etc… Alors que la classe Filtre contient du code ayant vocation a être compilé pour la cible microcontrôleur et est donc limité en termes d'utilisation de librairie et de ressources matérielles, il n'y a pas de telles limitations pour la classe FiltreTrace. Les membres de la classe FiltreTrace sont déclarés dans le fichier filtretrace.h et l'implémentation des méthodes est réalisée dans le fichier filtretrace.cpp

Pour rappel, il est possible en C++ de définir des valeurs par défaut pour les paramètres des méthodes. La valeur de ces paramètres est définie dans la définition de la méthode (fichier .h). Dans l'implémentation des méthodes (fichier .cpp), ces valeurs par défaut n'apparaissent pas. Lors de l’invocation, si la valeur effective d'un paramètre n'est pas fournie, le paramètre est affecté à sa valeur par défaut.

Le pointeur memoireVk dans la classe Filtre peut être alloué dynamiquement par le constructeur de la classe et sera donc utilisé comme un tableau de taille nbMemoireVk dans votre code.

Jusqu'à ce TP, vous avez utilisé la méthode void FiltreTrace::Reponse(double * ek, double * sk, int nbPts) pour appliquer le calcul de la réponse d'un filtre. Pour réaliser un filtre capable de traiter des échantillons en ligne, il faut que le processeur effectue le calcul de l'équation de récurrence échantillon par échantillon. La première partie du TP consiste donc à implémenter la méthode echantillon_t Filtre::TraiteUnEchantillon(echantillon_t ek) qui réalise le calcul de cette équation de récurrence.

Afin de pouvoir tester cette méthode, la méthode void FiltreTrace::ReponseEnLigne(echantillon_t * e, echantillon_t * s, int nbPts) doit :

1. invoquer la méthode void Filtre::ResetMemoireVk()
2. traiter tous les échantillons du tableau e (pour $k\in[0,nbPts-1]$) à l'aide de la méthode echantillon_t Filtre::TraiteUnEchantillon(echantillon_t ek) et ranger le résultat dans le tableau s

Le code d'une version simplifiée de la méthode void FiltreTrace::ReponseEnLigne(echantillon_t * e, echantillon_t * s, int nbPts) est montré ci dessous (Vous n'avez pas à changer le code présent dans le fichier filtretrace.cpp):

void FiltreTrace::ReponseEnLigne(echantillon_t * e, echantillon_t * s, int nbPts)
{
    ResetMemoireVk();
    for (int k=0; k < nbPts; k++)    {
        s[k] = TraiteUnEchantillon(e[k]);
    }
}

Lire le code de la méthode void FiltreTrace::ReponseEnLigne et répondez aux questions suivantes sur le compte rendu :

1. que représentent e et s ? (indice : la même chose que pour la méthode calculReponseFiltre() )
2. que représentent e[0] et s[0] ?
3. que faut-il ranger dans la case s[k] ?

Implémenter la méthode echantillon_t Filtre::TraiteUnEchantillon pour qu'elle retourne la valeur de l'échantillon e_k multiplié par 3. Compiler et exécuter le programme. Justifier sur le compte-rendu les réponses affichées à l'écran. Quelle est l'équation correspondant à ce filtre ?

Une fois les réponses validées, mettre à jour le suivi de version en saisissant dans une console:

echo commence
cd ~/TP_ARCHI_TNS_ETU
git commit -a -m'first filter working'
gitk & 
echo fini

On cherche maintenant à implémenter l'équation: 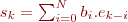$s_k=\sum_{i=0}^{N}b_i.e_{k-i}$.

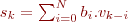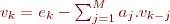Afin de faciliter la transition vers la réalisation des filtres RII, on codera la forme canonique $s_k=\sum_{i=0}^{N}b_i.v_{k-i}$ avec $v_k=e_k-\sum_{j=1}^{M}a_j.v_{k-j}$. Mais comme pour les filtres RIF 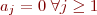$a_j=0\; \forall j\geq1$ on obtient simplement dans ce cas $v_k=e_k$

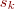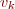Pour calculer $s_k$, il est nécessaire de disposer des valeurs des coefficients du filtres $b_i$ et des échantillons $v_k$ courant et précédents, stockés dans un buffer circulaire tel que présenté dans le cours.

La figure suivante illustre le fonctionnement d'un tel buffer de taille 6:

Le tableau memoireVk est utilisé pour stocker les échantillons. L'attribut d'instance indice_ecr est utilisé pour indiquer le numéro (indice d'écriture) de la case dans laquelle ranger l'échantillon le plus récent. Dans le codage, vous tiendrez compte du fait que le tableau memoireVk est circulaire et de taille nbMemoireVk éléments pour la mise à jour des indices de lecture et d'écriture.

Compléter la méthode echantillon_t Filtre::TraiteUnEchantillon(echantillon_t ek) pour qu'elle:

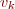1. calcule $v_k$ à partir de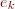 $e_k$
2. range l'échantillon 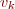$v_k$ au bon endroit dans le buffer circulaire.
3. calcule la valeur de 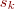$s_k$, conformément à la formule rappelée en début d'exercice, en remontant les échantillons à partir de 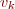$v_k$. Pour cela, vous utiliserez une variable locale servant d'indice de lecture (revoir le TD1 d'architecture…). Les coefficients du filtre sont au nombre de nbCoeffB et leurs valeurs se trouvent dans le tableau pCoeffB.
4. prépare l'itération suivante en mettant à jour l'indice d'écriture.

Tester votre méthode à l'aide du filtre dont les coefficients sont définis dans le tableau coeffB du fichier tparchi1.cpp.

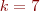Vérifier l'exactitude des réponses impulsionnelles et indicielles pour le filtre fourni jusque $k=7$ en comparant les échantillons en sortie du filtre avec les valeurs que vous calculerez sur votre compte-rendu. Conclure.

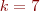Vérifier l'exactitude des réponses impulsionnelles et indicielles pour le filtre fourni jusque $k=7$ à l'aide d'un test automatique en invoquant cette ligne après filtre_echo_RIF.ReponseEnLigne(…) dans la fonction code_tparchi1() :

  double errmax=filtre_echo_RIF.CompareReponses(impulsion,NB_ECH);

La variable errmax fournit alors l'erreur maximale entre l'implémentation de référence (fournie par les enseignants) et la votre. Elle doit être (quasi) nulle pour valider votre code. Cette valeur est visible dans la console, (onglet Sortie de l'application, en bas de la fenêtre de QtCreator).

Appliquer ce filtre à deux sinusoïdes de fréquence 50 Hz et 500 Hz (en considérant la fréquence d'échantillonage à 5Khz). Pour cela, vous devrez ajouter ces signaux à coté de l'impulsion et de l'échelon. Expliquez le résultat en vous aidant du module de la fonction de transfert.

Une fois les réponses validées, mettre à jour le suivi de version en saisissant dans une console:

echo commence
cd ~/TP_ARCHI_TNS_ETU
git commit -a -m'RIF working'
gitk & 
echo fini

On cherche maintenant à implémenter l'équation: 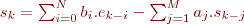$s_k=\sum_{i=0}^{N}b_i.e_{k-i}-\sum_{j=1}^{M}a_j.s_{k-j}$.

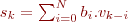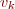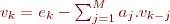Pour cela, nous utiliserons la forme canonique vue en cours: $s_k=\sum_{i=0}^{N}b_i.v_{k-i}$ faisant intervenir les termes $v_k$. Pour l'échantillon $k$, il est nécessaire d'évaluer la valeur de $v_k=e_k-\sum_{j=1}^{M}a_j.v_{k-j}$ qui utilise les valeurs des 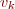$v_k$ précédemment calculés.

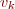Compléter la méthode echantillon_t Filtre::TraiteUnEchantillon(echantillon_t ek) pour qu'elle permette de gérer ce type de filtre. Pour cela, vous devez modifier le calcul de $v_k$ réalisé à l'étape 1. de l'exercice 2 ainsi :

1. calculer 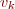$v_k$ à partir des valeurs précédentes de 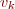$v_k$ stockées dans le tableau memoireVk. Vous utiliserez le même principe que pour le calcul de 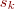$s_k$ réalisé pour le filtre RIF. Les coefficients du filtre à utiliser sont au nombre de nbCoeffA et sont situés dans le tableau pCoeffA.

Tester l'implémentation de la méthode de calcul sur le filtre graĉe à un filtre simple de votre choix (voir les TP de TNS si vous êtes en panne d'inspiration)

Déclarer les variables nécessaires pour ajouter un second filtre d'équation de récurrence: $ s_k=e_k+0.3s_{k-7} $

Calculer les réponses impulsionnelles et indicielles en utilisant la méthode Filtre::ReponseEnLigne(echantillon_t * ek, echantillon_t * sk, int nbPts) et ajouter le code permettant de les afficher. Activer l'affichage du module de la fonction de transfert de ce filtre en supprimant dans le fichier tparchi1.cpp la ligne if(0) avant le commentaire:

//SUPPRIMER LA LIGNE SUIVANTE POUR POUVOIR OBSERVER LES RÉPONSES FRÉQUENTIELLES À PARTIR DE L'EXERCICE 2
  

Vérifier l'exactitude des réponses obtenues grâce à une des deux méthodes expliquées à l'exercice 2 jusqu'à l'échantillon 15.

Une fois les réponses validées, mettre à jour le suivi de version en saisissant dans une console:

echo commence
cd ~/TP_ARCHI_TNS_ETU
git commit -a -m'RII working'
gitk & 
echo fini

Bravo, vous pouvez maintenant passer au TP2: tptns2018_2