Table des matières
TP OML AII LIDAR
Contexte
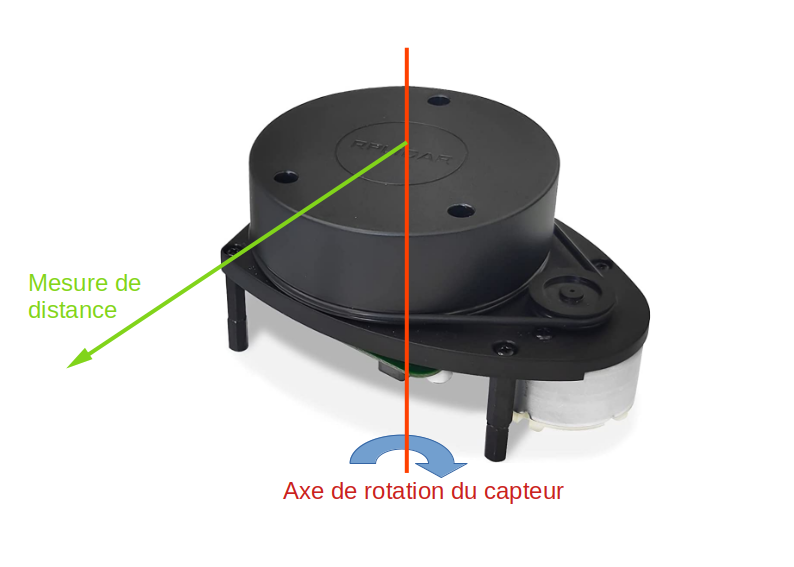
Dans ce TP de 4h, nous allons illustrer l'usage du calcul matriciel pour traiter des données issues d'un télémètre laser (LIDAR) à balayage. Ce type de capteur réalise des mesures de distance grâce à la durée nécessaire pour que la lumière effectue le trajet aller/retour du capteur à l'obstacle le plus proche. Le capteur de distance est lui même mis en rotation autour d'un axe pour réaliser un balayage angulaire afin d'effecteur des mesures dans différentes directions et former ainsi un nuage de points 2D. Le capteur est visible sur la figure suivante:
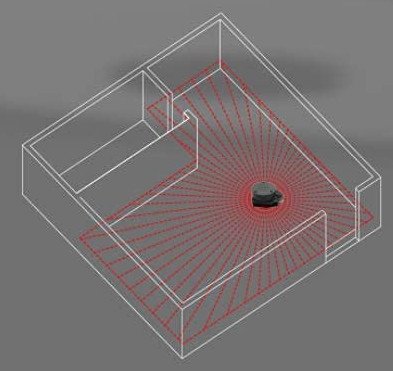
L'image suivante montre le capteur placé dans un environnement d'intérieur de bâtiment ainsi que les trajets optiques correspondant aux mesures dans différentes directions:
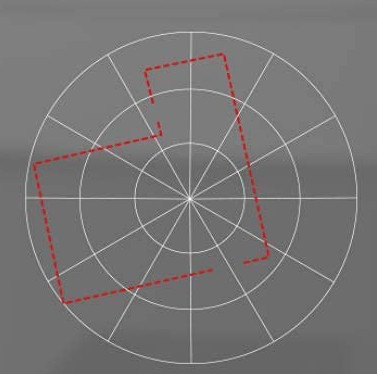
Chaque mesure de distance dans la scène est associée à une mesure angulaire, les deux infomations formant des coordonnées polaires. L'image suivante représente l'environnement tel qu'il est perçu par le capteur lors d'une rotation d'un tour, sous forme d'un nuage de points 2D affichés en coordonnées cartésiennes, centrés sur le capteur:
Durant ce TP, vous devrez:
- prendre en main une librairie de calcul matriciel appelée numpy
- détecter des segments de droites dans les données issues du télémètre
- déterminer le déplacement d'un capteur entre deux captures différentes effectuées par le capteur
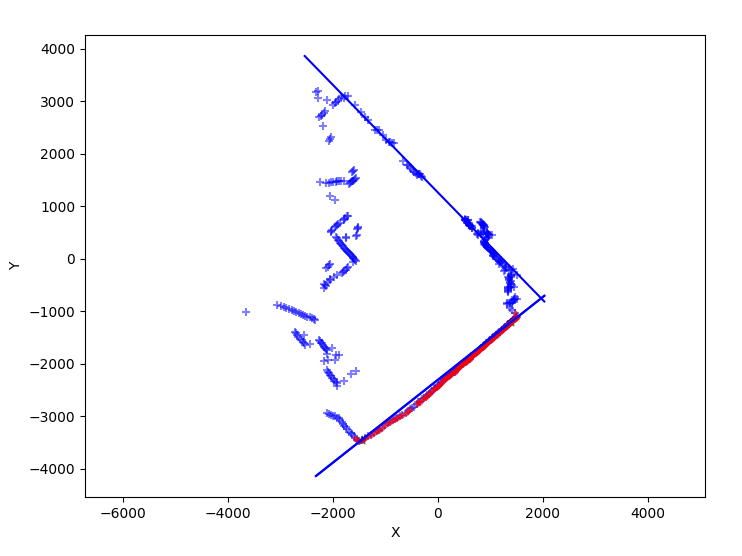
Cette figure représente les données d'un scan ainsi que 2 droites détectées:
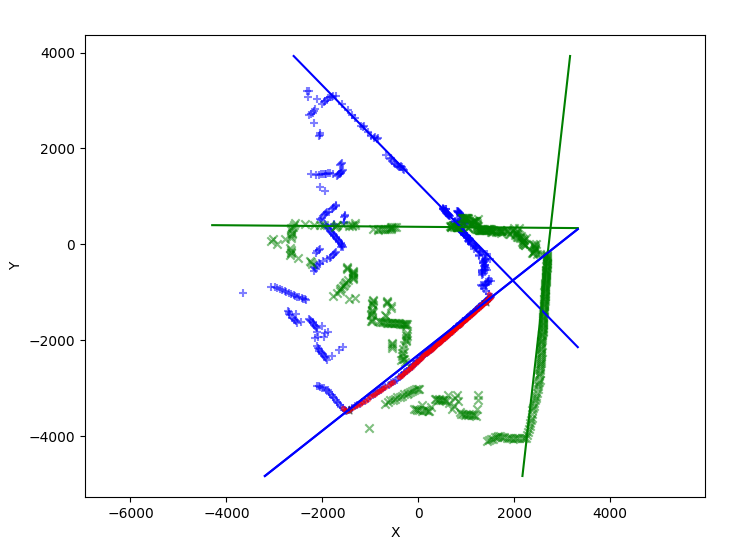
Cette figure représente les données de deux scans ainsi que 2 droites détectées dans chaque scan:
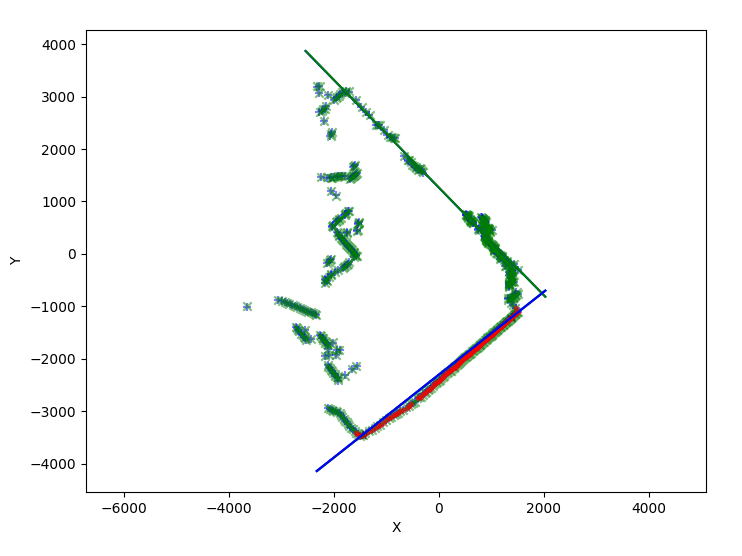
Cette figure représente les données des mêmes scans après recalage grâce à la mise en correspondances des 2 paires de droites:
Documentation de numpy
Ouvrir dans un autre onglet la documentation suivante: https://bvdp.inetdoc.net/files/iut/tp_oml1/numpy-user-1.23.0.pdf
Démarrage du projet
Installation des paquets PIP
Si nécessaire, installer les paquets pip suivants: Touche Windows+R
cmd pip install numpy pip install matplotlib
Rapatriement du projet et installation des extensions Python pour Visual Studio Code
Créer un dossier tpomllidar dans votre dossier P:\s5aii\s5aii1\nom_prenom\…
Télécharger les 2 fichiers squelettes python suivants dans votre dossier P:\s5aii\s5aii1\nom_prenom\tpomllidar\ (en faisant clic droit sur le nom du fichier et “enregistrer le lien sous”…):
- tpoml1.py
#B. Vandeportaele 2022 #Squelette de programme pour TP OML LIDAR #IUT GEII TOULOUSE #Importation librairie pour fabs, sqrt, cos, sin ... import math #Importation librairie pour le calcul numérique, matrices etc... et affichage de la version import numpy as np print("numpy version "+np.__version__) #Importation librairie pour l'affichage #https://matplotlib.org/stable/tutorials/introductory/pyplot.html import matplotlib.pyplot as plt ############################################################################################## # Fonction fournie pour l'affichage des informations pour une matrice np.ndarray # Il n'est pas nécessaire de regarder le code, il suffit d'uiliser la fonction affiche(...) # en lui passant en premier paramètre la matrice à afficher # le second paramètre optionnel est une chaine de caractères pour contextualiser l'affichage import inspect def affiche(mat,chaine_prefix=""): def mod_retrieve_name(var): #récupéré sur https://stackoverflow.com/questions/18425225/getting-the-name-of-a-variable-as-a-string et https://ideone.com/ym3bkD callers_local_vars = inspect.currentframe().f_back.f_back.f_locals.items() return [var_name for var_name, var_val in callers_local_vars if var_val is var] #ajoute un espace après la chaine de prefix si besoin if chaine_prefix!="" and chaine_prefix[-1]!=" ": chaine_prefix=chaine_prefix+" " matName= mod_retrieve_name(mat) if isinstance(mat,np.ndarray): print(chaine_prefix + str(matName) + " shape: "+str(mat.shape) + " ndim: "+str(mat.ndim) + " dtype: "+str(mat.dtype)+ " valeurs: \n"+str(mat)) else: print(chaine_prefix + str(matName) + " n'est pas une matrice") if isinstance(mat,str): print(mat) ############################################################################################## ############################################################################################## # Fonction fournie pour l'affichage d'une droite # Il n'est pas nécessaire de regarder ce code # définition des limites pour l'affichage par défaut: # xmin,xmax,ymin,ymax=-100,100,-100,100 def affiche_droite(da,db,dc,style='r-',xmin=-100,xmax=100,ymin=-100,ymax=100): def ci(a1,b1,c1,a2,b2,c2): A=np.array([[a1,b1], [a2,b2]],dtype = float) B=np.array([[-c1], [-c2]],dtype = float) if np.linalg.matrix_rank(A)==2: X=np.linalg.inv(A)@B else: X=np.array([[np.inf], [np.inf]],dtype = float) return X ''' plot_intersection(da,db,dc,0,1,-ymin) plot_intersection(da,db,dc,0,1,-ymax) plot_intersection(da,db,dc,1,0,-xmin) plot_intersection(da,db,dc,1,0,-xmax) ''' #def plot_intersection(a1,b1,c1,a2,b2,c2): #plt.scatter(X[0],X[1],marker='+',color='red',alpha=0.5) X1=ci(da,db,dc,0,1,-ymin) X2=ci(da,db,dc,0,1,-ymax) X3=ci(da,db,dc,1,0,-xmin) X4=ci(da,db,dc,1,0,-xmax) #cherche les 2 points les plus près du centre de la figure C=np.array([[(xmax+xmin)/2], [(ymax+ymin)/2]],dtype = float) #plt.scatter(C[0],C[1],marker='*',color='black',alpha=0.5) # https://numpy.org/doc/stable/reference/generated/numpy.linalg.norm.html XX=np.array([ [X1],[X2],[X3],[X4]]).reshape(4,2) d1=np.linalg.norm(X1-C) d2=np.linalg.norm(X2-C) d3=np.linalg.norm(X3-C) d4=np.linalg.norm(X4-C) listd=np.array([d1,d2,d3,d4],dtype = float) #récupère en 0 et 1 les indices des 2 plus petites distances idx=np.argsort(listd) #print(f"idx:{idx}") x1=XX[idx[0],0] x2=XX[idx[1],0] y1=XX[idx[0],1] y2=XX[idx[1],1] plt.plot([XX[idx[0],0], XX[idx[1],0] ], [XX[idx[0],1], XX[idx[1],1] ], style) ############################################################################################## # Fonction permettant de comparer 2 droites (da,db,dc) et (das,dbs,dcs) #retourne vrai si les 2 droites sont identiques, faux sinon def compare_droite(da,db,dc,das,dbs,dcs): #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- return False #valeur par défaut ############################################################################################## def determine_droite(pointsSegmentX, pointsSegmentY): #valeurs par défaut: da,db,dc=1,0,0 if len(pointsSegmentX)==2: print("Cas de l'ajustement de droite sur 2 points") x1=float(pointsSegmentX[0]) y1=float(pointsSegmentY[0]) x2=float(pointsSegmentX[1]) y2=float(pointsSegmentY[1]) if x1==x2 and y1==y2: print("Determine_droite(...) appelée avec 2 points identiques... ") return None #exit(-1) #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- else: print("Cas de l'ajustement de droite sur plus de 2 points") #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- #normalisation pour avoir norme de (da,db)=1 n=math.sqrt((da*da)+(db*db)) da=da/n db=db/n dc=dc/n return da,db,dc #################################################################### def test_determine_droite(): print("test_determine_droite()") #test de la fonction determine_droite avec 2 points identiques fournis, elle doit retourner None print("test1") if determine_droite([0,0],[1,1]) is None: print(f"test réussi") else: print(f"test échoué") #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- #################################################################### #------------------------------------------- def calcule_distance_droite_a_point(a,b,c,x,y): #à coder à partir de l'explication sur https://homeomath2.imingo.net/distance2.htm #vous pouvez utiliser math.fabs() et math.sqrt() d=0 #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- return d #------------------------------------------- def test_calcule_distance_droite_a_point(): print("test_calcule_distance_droite_a_point") d1=calcule_distance_droite_a_point(1,0,0,3,0) # x=0 / (3,0) print(f"d1 obtenu: {d1} / attendu {3}") d1=calcule_distance_droite_a_point(0,1,0,3,0) # y=0 / (3,0) print(f"d1 obtenu: {d1} / attendu {0}") d1=calcule_distance_droite_a_point(1,1,1,0,0) # x+y+1=0 / (0,0) print(f"d1 obtenu: {d1} / attendu {math.sqrt(2)/2}") #------------------------------------------- def calcule_intersection(a1,b1,c1,a2,b2,c2): #position X=[x,y] de l'intersection des deux droites X=np.array([[0], [0]],dtype = float) #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- return X #------------------------------------------- def plot_intersection(a1,b1,c1,a2,b2,c2): X=calcule_intersection(a1,b1,c1,a2,b2,c2) plt.scatter(X[0],X[1],marker='+',color='red',alpha=0.5) #------------------------------------------- def test_calcule_intersection(): print("test_calcule_intersection()") #test1 a1,b1,c1,a2,b2,c2=0,1,3,4,0,2 affiche_droite(a1,b1,c1,style='r-') affiche_droite(a2,b2,c2,style='r-') X=calcule_intersection(a1,b1,c1,a2,b2,c2) affiche(X) plt.scatter(X[0],X[1],marker='x',color='red',alpha=0.5) if not (X[0]==-0.5 and X[1]==-3): print("test1 échoué") #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- ################################################################ def essai_paire_ransac(scan,indice1,indice2,seuil_distance): #calcul de la droite à partir de 2 points points_segment_test_X=[scan[indice1][0],scan[indice2][0]] points_segment_test_Y=[scan[indice1][1],scan[indice2][1]] da,db,dc=determine_droite(points_segment_test_X, points_segment_test_Y) #collecte les points du scan correspondant à cette droite et les compte points_segment_X=[] points_segment_Y=[] somme_score=0 for s in scan: x=s[0] y=s[1] distance=calcule_distance_droite_a_point(da,db,dc,x,y) if distance<seuil_distance: points_segment_X.append(x) points_segment_Y.append(y) score=1 else: score=0 somme_score=somme_score+score return somme_score ################################################################ def ransac(scan,seuil_distance,nombre_tirages_aleatoires=100): #pour avoir la même séquence pseudo aléatoire à chaque test np.random.seed(168) score_maxi= 0. indices_maxi=np.array([0,0], dtype=int) nb_mesures=len(scan) for iteration in range(nombre_tirages_aleatoires): indices=np.array([0,0], dtype=int) #tirage aléatoire de 2 indices différents while(indices[0]==indices[1]): indices=np.random.randint(0,nb_mesures,2) score=essai_paire_ransac(scan,indices[0],indices[1],seuil_distance) #print(f"indices tirés aléatoirement: {indices} {type(indices)}, score: {score}") if score>score_maxi: score_maxi=score indices_maxi[0]=indices[0] indices_maxi[1]=indices[1] return indices_maxi[0],indices_maxi[1] ################################################################ def test_ransac(): #liste de points 2D vide scan1=[] #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- #définir une droite de votre choix dans la zone affichable (x et y compris entre -100 et +100) #modifier ces valeurs, avec b non nul: a,b,c=0.1,0.8,40 amplitude_perturbation=0 nombre_points_outliers=0 #générer 200 points échantillonnés sur cette droite dans la zone affichable (x et y compris entre -100 et +100) #et les ajouter à la liste avec scan1.append([x,y]) for n in range(-100,100,1): #TODO: générer des points sur la droite x=0 y=0 #ajout d'une perturbation au point x=x+amplitude_perturbation*float(np.random.randn(1)) y=y+amplitude_perturbation*float(np.random.randn(1)) scan1.append([x,y]) #ajout de données aberrantes: les outliers for n in range(0,nombre_points_outliers): #tirage aléatoire d'un point x=-100+200*float(np.random.rand(1)) y=-100+200*float(np.random.rand(1)) scan1.append([x,y]) scan1X=[] scan1Y=[] for s in scan1: scan1X.append(s[0]) scan1Y.append(s[1]) if len(scan1)>=2: plt.scatter(scan1X,scan1Y,marker='+',c="blue",alpha=0.5) i1,i2=ransac(scan1,10) da,db,dc=determine_droite([scan1[i1][0],scan1[i2][0]],[scan1[i1][1],scan1[i2][1]]) affiche_droite(da,db,dc,style='r-') compare_droite(da,db,dc,a,b,c) ################################################################ #Préparation des données pour egomotion ################################################################ #Importation d'un fichier python contenant les données d'un scan: import scan000001 as sc #copie des données importées vers une variable globale utilisable par ce programme scan_polaire=sc.donnees nb_mesures=len(scan_polaire) print("Le scan contient: "+str(nb_mesures)+ " mesures") #conversion des données de coordonnées polaires vers coordonnées cartésiennes scan1=[] for m in scan_polaire: if m[1]!=0: #les données avec mesure de distance à 0 sont des trous x=m[1]*math.cos(m[0]*math.pi/180.) y=m[1]*math.sin(m[0]*math.pi/180.) scan1.append([x,y]) #génère des données que percevrait le capteur après deplacement theta=0.789 dx=841.3 dy=-521.0 #matrice de changement de repère en coordonnées homogènes: M_2_1=np.array( [ [math.cos(theta), -math.sin(theta), dx] , [math.sin(theta), math.cos(theta) , dy] , [0 , 0 , 1] ]) affiche(M_2_1) #application de la transformation au scan1 scan2=[] for m in scan_polaire: if m[1]!=0: #les données avec mesure de distance à 0 sont des trous #TODO: verifier le sens de rotation du capteur (peut être faut il - sur l'angle pour convertir en cartésien) x=m[1]*math.cos(m[0]*math.pi/180.) y=m[1]*math.sin(m[0]*math.pi/180.) p1=np.array( [x , y , 1 ]).reshape(3,1) p2=M_2_1@p1 #affiche(p2) #ajout d'un bruit gaussien d'écart type 3 sur les coordonnées des points A = 3* np.random.randn(2).reshape(2,1) scan2.append([float(p2[0]+A[0]), float(p2[1]+A[1]) ]) #choix des indices de 2 points pour l'estimation des deux droites dans les deux scans #ici les indices sont les mêmes pour les deux scans, i1=295 #point 1 droite 1 i2=405 #point 2 droite 1 i3=103 #point 1 droite 2 i4=455 #point 2 droite 2 ################################################################ def affiche_scan(scan1,scan2=None): global i1,i2,i3,i4 scan1X=[] scan1Y=[] scan2X=[] scan2Y=[] scan1et2X=[] scan1et2Y=[] for s in scan1: scan1X.append(s[0]) scan1Y.append(s[1]) scan1et2X.append(s[0]) scan1et2Y.append(s[1]) if scan2 != None: for s in scan2: scan2X.append(s[0]) scan2Y.append(s[1]) scan1et2X.append(s[0]) scan1et2Y.append(s[1]) #détermination des limites pour l'affichage, dépassement de 10% de chaque coté xmin=min(scan1et2X)-(max(scan1et2X)-min(scan1et2X))*0.1 xmax=max(scan1et2X)+(max(scan1et2X)-min(scan1et2X))*0.1 ymin=min(scan1et2Y)-(max(scan1et2Y)-min(scan1et2Y))*0.1 ymax=max(scan1et2Y)+(max(scan1et2Y)-min(scan1et2Y))*0.1 fig = plt.figure(figsize=(8, 6)) axes = plt.axes() axes.set_xlim([xmin,xmax]) axes.set_ylim([ymin,ymax]) axes.axis('equal') #https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.scatter.html plt.scatter(scan1X,scan1Y,marker='+',c="blue",alpha=0.5) plt.scatter(scan2X,scan2Y,marker='x',c="green",alpha=0.5) #trace les droites detectées dans les 2 scans da11,db11,dc11=determine_droite( [scan1X[i1],scan1X[i2]] , [scan1Y[i1],scan1Y[i2]] ) da12,db12,dc12=determine_droite( [scan1X[i3],scan1X[i4]] , [scan1Y[i3],scan1Y[i4]] ) affiche_droite(da11,db11,dc11,'b-',xmin,xmax,ymin,ymax) affiche_droite(da12,db12,dc12,'b-',xmin,xmax,ymin,ymax) if scan2 is not None: da21,db21,dc21=determine_droite( [scan2X[i1],scan2X[i2]] , [scan2Y[i1],scan2Y[i2]] ) da22,db22,dc22=determine_droite( [scan2X[i3],scan2X[i4]] , [scan2Y[i3],scan2Y[i4]] ) affiche_droite(da21,db21,dc21,'g-',xmin,xmax,ymin,ymax) affiche_droite(da22,db22,dc22,'g-',xmin,xmax,ymin,ymax) pointsSegmentX=[scan1X[i1],scan1X[i2]] pointsSegmentY=[scan1Y[i1],scan1Y[i2]] plt.xlabel('X') plt.ylabel('Y') plt.show() ################################################################ def ego_motion(scan1,scan2): global i1,i2,i3,i4 #paramètres de la transformation à calculer, valeurs par défaut theta, dx, dy=0,0,0 M_2_1=np.array( [ [math.cos(theta), -math.sin(theta), dx] , [math.sin(theta), math.cos(theta) , dy] , [0 , 0 , 1] ]) M_1_2=np.linalg.inv(M_2_1) scan1X=[] scan1Y=[] scan2X=[] scan2Y=[] for s in scan1: scan1X.append(s[0]) scan1Y.append(s[1]) for s in scan2: scan2X.append(s[0]) scan2Y.append(s[1]) da11,db11,dc11=determine_droite( [scan1X[i1],scan1X[i2]] , [scan1Y[i1],scan1Y[i2]] ) da12,db12,dc12=determine_droite( [scan1X[i3],scan1X[i4]] , [scan1Y[i3],scan1Y[i4]] ) da21,db21,dc21=determine_droite( [scan2X[i1],scan2X[i2]] , [scan2Y[i1],scan2Y[i2]] ) da22,db22,dc22=determine_droite( [scan2X[i3],scan2X[i4]] , [scan2Y[i3],scan2Y[i4]] ) #intersection de D1 et D2 dans scan1 I1=calcule_intersection(da11,db11,dc11,da12,db12,dc12) X1=float(I1[0]) Y1=float(I1[1]) #intersection de D1 et D2 dans scan2 I2=calcule_intersection(da21,db21,dc21,da22,db22,dc22) X2=float(I2[0]) Y2=float(I2[1]) #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- #affichage des paramètres calculés print(f"dx calculé:{dx} , dy calculé:{dy} , theta calculé:{theta} ") #applique la transformation M_1_2 au scan2 et retourne le scan2 transformé scan2_transforme=[] for s in scan2: scan2X.append(s[0]) scan2Y.append(s[1]) x=s[0] y=s[1] p2=np.array( [x , y , 1 ]).reshape(3,1) p1=M_1_2@p2 scan2_transforme.append([float(p1[0]), float(p1[1]) ]) return scan2_transforme ################################################################ ######################################### def affichage_tests_etudiant(): fig = plt.figure(figsize=(8, 6)) axes = plt.axes() #axes.set_xlim([xmin,xmax]) #axes.set_ylim([ymin,ymax]) axes.axis('equal') #https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.scatter.html #exemple de tracé de droite en cyan: affiche_droite(1,0,1,'c-') #pour effacer la figure, vous pouvez utiliser: #plt.clf() #------------------------------------------------------------------- # CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- #------------------------------------------------------------------- # FIN DU CODE A COMPLETER PAR LES ETUDIANTS #------------------------------------------------------------------- plt.xlabel('X') plt.ylabel('Y') plt.show() exit() #arrete le programme à la fin de la fonction ######################################### affichage_tests_etudiant() #le code suivant n'est executé que si affichage_tests_etudiant() n'est pas exécuté: #modifie scan2 après estimation du changement de pose scan2=ego_motion(scan1,scan2) affiche_scan(scan1,scan2)
Ouverture du projet
Lancer Visual Studio Code
Cliquer sur Fichier→open Folder et choisir le dossier “P:\s5aii\s5aii1\nom_prenom\tpomllidar”
Cliquer sur “Yes I trust the Authors”
Cliquer sur le fichier tpoml1.py et presser sur F5 pour lancer
Si la question “You don't have an extension for debugging python…” apparait, cliquer sur “Find Python Extension”
Dans la colonne de gauche, cliquer sur “install” à coté de “Python Intellisense…” puis en bas à droite sur “Install”
Gestion des droites
Pour le premier TP, vous devrez appeler vos fonctions de test à la suite à l'endroit indiqué dans la fonction affichage_tests_etudiant().
Choix de paramétrisation des droites
Afin de manipuler les droites dans le programme, nous n'utiliserons pas les équations de droites affines sous la forme 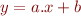 car cette forme ne permet pas de représenter à la fois des droites horizontales et verticales.
car cette forme ne permet pas de représenter à la fois des droites horizontales et verticales.
Nous utiliserons ici la forme 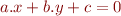 . Avec cette paramétrisation:
. Avec cette paramétrisation:
- le vecteur directeur est réglé par les paramètres
 et
et  (
(  est le vecteur normal à la droite)
est le vecteur normal à la droite) - la distance à l'origine est réglée par
 (mais pas forcement égale à)
(mais pas forcement égale à)
L'équation peut être multipliée par tout réel non nul sans changer la droite qu'elle représente:
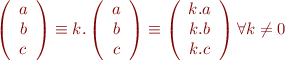
Dans le cas ou 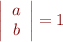 alors
alors  est égal à la distance de la droite à l'origine.
est égal à la distance de la droite à l'origine.
Prise en main de la paramétrisation des droites et affichage
Dans le squelette fourni se trouve une fonction affiche_droite(da,db,dc,style='r-',xmin=-100,xmax=100,ymin=-100,ymax=100) permettant d'afficher des droites dans une fenêtre.
Compléter la fonction affichage_tests_etudiant() à l'endroit indiqué afin d'afficher des droites dont vous aurez préalablement choisi les paramètres, l'affichage se faisant dans un carré de coté 200 centré sur 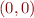 . Le style pourra être réglé à 'b-','m-','y-','g-','c-','k-' pour choisir la couleur et différentier les droites. Vous devrez appeler toutes les différentes fonctions de test depuis affichage_tests_etudiant(). Pour effacer l'affichage graphique après un test, vous pourrez utiliser: plt.clf()
. Le style pourra être réglé à 'b-','m-','y-','g-','c-','k-' pour choisir la couleur et différentier les droites. Vous devrez appeler toutes les différentes fonctions de test depuis affichage_tests_etudiant(). Pour effacer l'affichage graphique après un test, vous pourrez utiliser: plt.clf()
Comparaison des droites
Implémenter la fonction compare_droite(da,db,dc,das,dbs,dcs) afin qu'elle retourne true quand les droites  et
et  sont “suffisamment proche” et false sinon.
sont “suffisamment proche” et false sinon.
Ajustement d'une droite sur 2 points
Nous nous intéressons maintenant à la fonction determine_droite(pointsSegmentX, pointsSegmentY) prenant en paramètres:
- pointsSegmentX: une liste de coordoonées X des points
- pointsSegmentY: une liste de coordoonées Y des points
Cette fonction retourne None lorsque les 2 points fournis sont confondus. Dans le cas contraire, elle devra retourner les paramètres da,db,dc de la droite ajustée.
La fonction test_determine_droite() va nous servir à tester la fonction determine_droite(pointsSegmentX, pointsSegmentY) . Elle contient déjà un exemple de test fournissant 2 points confondus et vérifie que le résultat produit est correct. Appelez test_determine_droite() dans affichage_tests_etudiant() et vérifier que le test se déroule bien.
Ajouter ce test dans test_determine_droite() :
print("test2")
plt.scatter([0,1],[-1,0],marker='+',color='red',alpha=0.5)
da,db,dc=determine_droite([0,1],[-1,0])
if compare_droite(da,db,dc, -1,1,1)==False:
print(f"test échoué")
affiche_droite(da,db,dc,'r-')
et observer le résultat du test.
Vous devez maintenant compléter determine_droite(pointsSegmentX, pointsSegmentY): pour qu'elle puisse passer ce test. Vous pourrez dans un premier temps considérer que le paramètre  de la droite est égal à 1 (pour rappel, l'équation de droite est définie à un facteur d'échelle non nul près), il y aura donc 2 inconnues
de la droite est égal à 1 (pour rappel, l'équation de droite est définie à un facteur d'échelle non nul près), il y aura donc 2 inconnues  et
et  à déterminer. Pour cela vous devrez utiliser la librairie numpy afin de résoudre un système de 2 équations à 2 inconnues de la forme
à déterminer. Pour cela vous devrez utiliser la librairie numpy afin de résoudre un système de 2 équations à 2 inconnues de la forme  que vous construirez à l'aide des coordonnées des points fournis. Vous pourrez résoudre ce système en calculant
que vous construirez à l'aide des coordonnées des points fournis. Vous pourrez résoudre ce système en calculant 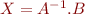 . Vous utiliserez la fonction zeros de numpy pour initialiser les matrices
. Vous utiliserez la fonction zeros de numpy pour initialiser les matrices  et
et  avant de les remplir avec les bonnes valeurs. De plus, vous penserez à déposer dans les paramètres de retour de la fonctions les valeurs extraites de
avant de les remplir avec les bonnes valeurs. De plus, vous penserez à déposer dans les paramètres de retour de la fonctions les valeurs extraites de  , en ayant pris soin de les caster en type float.
, en ayant pris soin de les caster en type float.
Vérifier le bon fonctionnement du test.
Ajouter ce test dans test_determine_droite() :
print("test3")
plt.scatter([-1,-2],[-1,-2],marker='+',color='blue',alpha=0.5)
da,db,dc=determine_droite([-1,-2],[-1,-2])
if compare_droite(da,db,dc, 1,-1,0)==False:
print(f"test échoué")
affiche_droite(da,db,dc,'b-')
et observer le résultat du test. Mettre en relation la propriété de la droite et le problème causé sur le système d'équations à résoudre.
Compléter determine_droite(pointsSegmentX, pointsSegmentY): pour qu'elle puisse passer ce test. Pour cela vous devrez vérifier le rang de la matrice  du système d'équations à l'aide de:
du système d'équations à l'aide de:
rang_a=np.linalg.matrix_rank(A)
Le traitement précédent fonctionne pour des matrices  de rang 2, il faut donc conditionner son exécution au fait que le rang de
de rang 2, il faut donc conditionner son exécution au fait que le rang de  soit de 2, et sinon exécuter un traitement différent adapté au cas particulier du rang de
soit de 2, et sinon exécuter un traitement différent adapté au cas particulier du rang de  égal à 1 qui signifie que les lignes de
égal à 1 qui signifie que les lignes de  ne sont pas linéairement indépendantes, autrement dit ici que l'une et l'autre sont égales à un facteur d'échelle près. Réfléchir à ce que cela implique pour la droite et proposer un traitement (très simple) pour calculer les paramètres
ne sont pas linéairement indépendantes, autrement dit ici que l'une et l'autre sont égales à un facteur d'échelle près. Réfléchir à ce que cela implique pour la droite et proposer un traitement (très simple) pour calculer les paramètres  ,
,  et
et  de la droite dans ce cas particulier.
de la droite dans ce cas particulier.
Vérifier le bon fonctionnement du test après avoir intégré vos modifications.
Ajouter ce test dans test_determine_droite() :
print("test4")
plt.scatter([0,0],[0,1],marker='+',color='green',alpha=0.5)
da,db,dc=determine_droite([0,0],[0,1])
if compare_droite(da,db,dc, -1,0,0)==False:
print(f"test échoué")
affiche_droite(da,db,dc,'g-')
et observer le résultat du test. Mettre en relation la propriété de la droite et le problème causé sur le système d'équations à résoudre. Au besoin, modifier votre fonction determine_droite(…) pour qu'elle passe ce test.
Ajouter 2 tests supplémentaires de votre choix dans la fonction test_determine_droite()
Calcul de la distance d'un point à une droite
Implémenter la fonction calcule_distance_droite_a_point(a,b,c,x,y) en vous inspirant du résultat de https://homeomath2.imingo.net/distance2.htm et en utilisant les fonctions math.fabs() et math.sqrt().
Utilisez la fonction test_calcule_distance_droite_a_point() fournie pour tester votre fonction calcule_distance_droite_a_point(a,b,c,x,y).
Calcul de l'intersection de deux droites
En vous inspirant de ce que vous venez de faire pour calculer la droite passant par deux points, compléter la fonction calcule_intersection(a1,b1,c1,a2,b2,c2) pour calculer le point à l'intersection de deux droites. Dans le cas particulier de droites parallèles, la fonction devra retourner un vecteur dont les deux composantes seront égales à l'infini à l'aide de np.inf.
Exécuter le programme de test de la fonction test_calcule_intersection() et vérifier le bon fonctionnement. Vous pourrez utiliser la fonction affiche(…) fournie pour afficher le résultat de calcule_intersection(…) car il s'agit d'un nd.array. Compléter le programme de test pour gérer un cas pour lequel le rang de la matrice du système d'équations sera égal à 1 et tester.
Ajustement d'une droite sur plus de 2 points
Nous allons maintenant enrichir la fonction determine_droite(pointsSegmentX, pointsSegmentY) pour qu'elle soit capable de calculer la droite passant au mieux par plus de 2 points.
Cette droite sera obtenue au sens des moindres carrés, ce qui signifie qu'elle minimisera la somme des distances au carrés aux différents points sur lesquels elle sera ajustée. Ainsi la valeur obtenue pour les paramètres  ,
,  et
et  optimum sont obtenus pour minimiser la somme des carrés des distances des points
optimum sont obtenus pour minimiser la somme des carrés des distances des points 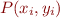 à la droite
à la droite 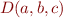 :
:
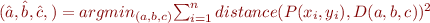
Comme pour le cas à 2 points, vous pourrez dans un premier temps considérer que le paramètre  de la droite est égal à 1 (pour rappel, l'équation de droite est définie à un facteur d'échelle non nul près), il y aura donc 2 inconnues
de la droite est égal à 1 (pour rappel, l'équation de droite est définie à un facteur d'échelle non nul près), il y aura donc 2 inconnues  et
et  à déterminer. Nous allons donc construire un système d'équations linéaires comme pour le cas à 2 points, mais nous allons y intégrer plus d'équations indépendantes que d'inconnues. Ce système
à déterminer. Nous allons donc construire un système d'équations linéaires comme pour le cas à 2 points, mais nous allons y intégrer plus d'équations indépendantes que d'inconnues. Ce système  n'admettra donc pas de solution au sens strict, mais en multipliant le système à gauche par
n'admettra donc pas de solution au sens strict, mais en multipliant le système à gauche par  , le système obtenu
, le système obtenu  peut être résolu avec
peut être résolu avec 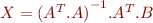 . La matrice
. La matrice 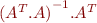 est appelée pseudo-inverse de
est appelée pseudo-inverse de  .
.
Pour construire les matrices  et
et  à partir des listes de points de taille variable, vous pourrez utiliser le code suivant:
à partir des listes de points de taille variable, vous pourrez utiliser le code suivant:
A=np.column_stack((pointsSegmentX, pointsSegmentY))) B=-np.ones((A.shape[0],1))
Pour calculer la solution du système, consulter la documentation de numpy.
Ajouter le test suivant dans test_determine_droite() et observer le résultat:
#test6 plt.scatter([10,20,30],[10,11,9],marker='+',color='green',alpha=0.5) da,db,dc=determine_droite([10,20,30],[10,11,9]) affiche_droite(da,db,dc,'g-')
Détection d'une droite dans un nuage de points
Le programme fourni contient 2 fonctions essai_paire_ransac(scan,indice1,indice2,seuil_distance) et ransac(scan,seuil_distance,nombre_tirages_aleatoires=100) . Lire le code et essayer de comprendre le fonctionnement de ces fonctions. Vous allez ensuite compléter la fonction test_ransac() pour générer des données et afficher les résultats.
Dans un premier temps, calculer les coordonnées x et y des points sur la droite paramétrée par  ,
,  et
et  dans la boucle qui fait varier
dans la boucle qui fait varier  de -100 à +100. Appeler le programme de test test_ransac() dans
affichage_tests_etudiant() et observer le résultat. La droite calculée doit passer par les points et “compare_droite: test réussi” doit s'afficher.
de -100 à +100. Appeler le programme de test test_ransac() dans
affichage_tests_etudiant() et observer le résultat. La droite calculée doit passer par les points et “compare_droite: test réussi” doit s'afficher.
Dans un second temps, régler amplitude_perturbation à 6 et relancer un test. Interpréter le résultat.
Finalement, régler nombre_points_outliers à 500 et relancer un test. Interpréter le résultat.
Egomotion: détermination de transformation rigide
Analyse
Nous cherchons maintenant à déterminer la transformation rigide entre 2 nuages de points
Pour cela, dans la partie du code Préparation des données pour le TP, nous:
- chargeons les données d'un scan vers une variable scan_polaire
- convertissons les données de coordonnées polaires vers coordonnées cartésiennes vers une variable scan1
- générons une transformation connue appliquée aux points de scan1 pour obtenir des données modifiées dans une variable scan2, auquel nous ajoutons des petites perturbations
- déterminons (manuellement ici) 2 paires de points dans chaque scan, chaque paire servant à déterminer une droite
Les paramètres de la transformation rigides sont:
 angle de rotation autour de l'axe vertical, réglé via la variable theta réglée dans test à 0.789 radians
angle de rotation autour de l'axe vertical, réglé via la variable theta réglée dans test à 0.789 radians translation selon
translation selon  dans le plan horizontal, réglé via la variable dx réglée dans test à 841.3cm
dans le plan horizontal, réglé via la variable dx réglée dans test à 841.3cm translation selon
translation selon  dans le plan horizontal, réglé via la variable dy réglée dans test à -521.0cm
dans le plan horizontal, réglé via la variable dy réglée dans test à -521.0cm
Nous utilisons ces paramètres dans la matrice de changement de repère suivante 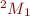 stockée dans la variable M_2_1 telle que:
stockée dans la variable M_2_1 telle que:
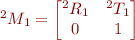 avec
avec 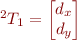 et
et 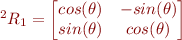
La fonction affiche_scan(scan1,scan2=None) fournie permet l'affichage en bleu du scan1 et en vert du scan2 ainsi que des droites correspondantes (calculées par votre fonction).
Commenter à la fin du fichier tpoml1.py l'appel de la fonction affichage_tests_etudiant(). Le programme va dorénavant appeler les fonctions ego_motion(scan1,scan2) et affiche_scan(scan1,scan2). Exécutez le programme avant de le modifier afin de voir les 2 scans non recalés (la fonction ego_motion(…) fournie applique une transformation sans effet sur le scan2 tant que vous ne l'avez pas modifiée). La ligne scan2=ego_motion(scan1,scan2) permet de procéder à l'appel de la fonction ego_motion(scan1,scan2) qui va devoir modifier le scan2 pour lui appliquer la transformation 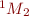 inverse de
inverse de 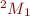 .
.
Pour cela, vous allez devoir utiliser les données disponibles suivantes:
- X1 et Y1 : coordonnées de l'intersection des 2 droites dans le scan1
- X2 et Y2 : coordonnées de l'intersection des 2 droites dans le scan2
- da11 et db11 : composantes du vecteurs normal d'une des droites dans le scan1
- da21 et db21 : composantes du vecteurs normal de la même droite dans le scan2
Écrire comment la matrice 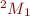 s'applique respectivement aux points et aux directions (vecteurs).
s'applique respectivement aux points et aux directions (vecteurs).
Nous allons tenter d'écrire sous forme matricielle  .
. =
= le système d'équations en regroupant dans
le système d'équations en regroupant dans  les inconnues à déterminer et dans
les inconnues à déterminer et dans  et
et  les données disponibles. Comme le terme
les données disponibles. Comme le terme  n'intervient pas en facteur mais à l'intérieur de fonctions trigonométriques, il n'est pas possible de mettre directement
n'intervient pas en facteur mais à l'intérieur de fonctions trigonométriques, il n'est pas possible de mettre directement  dans
dans  . Au lieu de cela, nous allons procéder à un changement de variables et déterminer
. Au lieu de cela, nous allons procéder à un changement de variables et déterminer 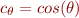 et
et 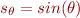 . Grâce à ce changement vous devriez être capable d'écrire le système sous forme matricielle et de déterminer
. Grâce à ce changement vous devriez être capable d'écrire le système sous forme matricielle et de déterminer  .
.
Pour calculer  à partir de
à partir de  et
et 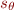 vous devrez:
vous devrez:
- vous assurer que
 et
et 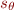 sont bien les cosinus et sinus d'un angle en vérifiant que
sont bien les cosinus et sinus d'un angle en vérifiant que 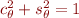
- puis utiliser la fonction angle=math.atan2(Y,X)
Codage
Compléter la fonction ego_motion(scan1,scan2) à l'endroit indiqué pour réaliser le calcul de la transformation 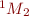 . Pour cela, coder les calculs que vous venez de réaliser, extraire les différents paramètres de
. Pour cela, coder les calculs que vous venez de réaliser, extraire les différents paramètres de  et reconstruire la matrice M_2_1 et l'inverser pour obtenir M_1_2. Dans le programme fourni, M_1_2 est appliqué au scan2 et si votre programme est correct, vous devriez voir les 2 scans se superposer en le relançant.
et reconstruire la matrice M_2_1 et l'inverser pour obtenir M_1_2. Dans le programme fourni, M_1_2 est appliqué au scan2 et si votre programme est correct, vous devriez voir les 2 scans se superposer en le relançant.
 Vous pouvez calculer la transformation
Vous pouvez calculer la transformation 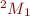 en écrivant un système comportant plus d'équations (6) que d'inconnues (4) utilisant les directions des deux autres droites et en résolvant le système obtenu au sens des moindres carrés.
en écrivant un système comportant plus d'équations (6) que d'inconnues (4) utilisant les directions des deux autres droites et en résolvant le système obtenu au sens des moindres carrés.
BONUS
image tirée de (mais il y avait une erreur sur la formule de R, qui est corrigée dans l'image): https://fr.planetcalc.com/8116/
Travail à faire et à rendre pour le 2 février
Utiliser la paramétrisation du cercle x0,y0=coordonnées du centre, r= rayon
- Faire la fonction determine_cercle avec 3 points en entrée
- Tester avec des données connues
- Augmenter la fonction determine_cercle pour plus de 3 points en entrée
- Générer des données synthétiques: des points sur un cercle avec perturbation réglable et nombre d'outliers réglable
- Mettre en place RANSAC pour trouver 1 cercle de rayon quelconque (tirer des triplets de points)
- Faire une fonction calcule_distance_cercle_a_point
- Générer des données synthétiques contenant 2 cercles de rayons connus r1 et r2
- Faire une fonction de recherche d'un cercle de rayon connu
- Mettre en place RANSAC pour trouver les 2 cercles de rayons connus r1 et r2 dans le nuage de points
- Effectuer la localisation (dx,dy,theta) du robot en fonction de la position observée de 2 cercles connus
Annexe
https://www.robot-maker.com/shop/capteurs/229-rp-lidar-a2-229.html
Projet C++ pour capturer les données avec le capteur: https://bvdp.inetdoc.net/wiki/doku.php?id=projets_capteurs_2022#rplidar
codage des nombres flottants en simple précision 32bits: https://www.h-schmidt.net/FloatConverter/IEEE754.html