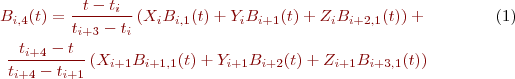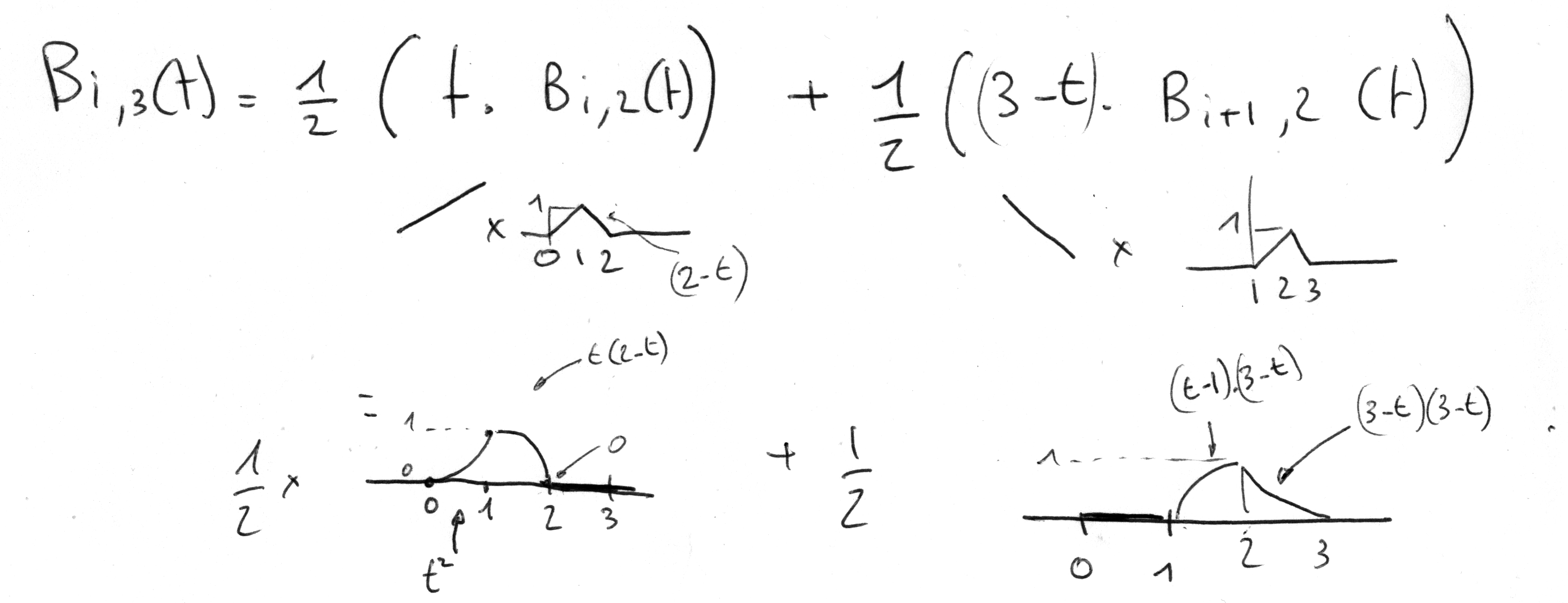Table des matières
Développement des fonctions de Bases pour splines cubiques non uniformes NUCS
site avec demo: http://www.inf.ed.ac.uk/teaching/courses/cg/d3/nonbspline.html
exercice: http://www.math.ucla.edu/~baker/pdf/pp_nonuniform.pdf
Papiers: https://theses.lib.vt.edu/theses/available/etd-100699-171723/unrestricted/chapter4.PDF
http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf
http://ftp.cs.wisc.edu/Approx/bsplbasic.pdf
http://www.maths.lse.ac.uk/Personal/jruf/papers/ruf_bspline.pdf
http://webee.technion.ac.il/Sites/People/YoninaEldar/Download/ME04c.pdf
https://fr.wikipedia.org/wiki/B-spline


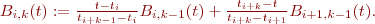
Implémentation Matlab
- nucs.m
function nucs( ) %Non-uniform cubic B-splines NON CUMULATIVES %b. Vandeportaele %d'après http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf close all clear all %%%%IMPORTANT%%%%%%%%% %pour spline linéaire %k=2 %pour spline quadratique %k=3 %pour spline cubique k=4;% pour avoir 3 fonctions de base non nulles entre t=3 et t=4. Il s'agit de B0 à B3 %j'affiche les fonctions de base en surnombre, mais en fait il suffit de %regarder les 4 fonctions de base sur l'intervale t=3 à t=4. et de %substituer les indices pour les P et les t for numerotest=1:2 figure hold on axis equal if numerotest==1 %pour distribution uniforme title('pour distribution uniforme'); P0=2; t0=0; P1=3; t1=1; P2=4; t2=2; P3=5; t3=3; %more points P4=6; t4=4; P5=7; t5=5; P6=8; t6=6; P7=9; t7=7; P8=10; t8=8; P9=11; t9=9; else %pour distribution non uniforme title('pour distribution non uniforme'); t1=1.1; t2=2.9; end %rangement dans des vecteurs listt=[t0;t1;t2;t3;t4;t5;t6;t7;t8;t9]; listp=[P0;P1;P2;P3;P4;P5;P6;P7;P8;P9]; %affichage des points de contrôle plot(listt, listp,'ko'); Base=zeros(4,1); for t=0:0.01:9 pt=0; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %pour indices de 0 à +3: plus simple à comprendre mais ne gère pas %bien les 3 premiers points de la spline; ce sera la version à %implémenter lorsque l'on changera les indices au fûr et à mesure %for i=0:5 % Base(i +1) = B( i,k,t,listt); % pt=pt+listp(i +1)*Base(i +1); %end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %pour indices de -2 à +5: permet une visu correcte de la courbe %pour qu'elle passe par les points de contrôle %je suis obligé de ranger les fonctions de bases en décalé... %je n'affiche pas ces 2 fonctions de base B-2 et B-1 sur la figure %mais elles sont utilisées pour le calcul de pt if k==2 indiceBaseMin=-1; elseif k==3 indiceBaseMin=-2; %ce n'est pas correct, il y a un offset... avec -1 aussi... ce n'est pas forcément grave car on s'intéresse aux splines cubiques else %k==4 indiceBaseMin=-2; end for i=indiceBaseMin:5 Base(-indiceBaseMin+ i +1) = B( i,k,t,listt); pt=pt+listp(-indiceBaseMin+ i +1)*Base(-indiceBaseMin+ i +1); end %Base %sum(Base) plot(t,Base(1),'gx'); plot(t,Base(2),'bx'); plot(t,Base(3),'kx'); plot(t,Base(4),'mx'); %affiche les fonctions de bases suivantes... plot(t,Base(5),'yx'); plot(t,Base(6),'cx'); %la courbe interpolée plot(t,pt,'r+'); end legend('PI','B0','B1','B2','B3','B4','B5','p(t)'); ylabel('p'); xlabel('t'); end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [ val ] = B( i,k,t,listt) %for first index=1 because of matlab if (i>=0) ti=listt(i + 1); else ti=listt(1); end if (i+1>=0) tip1=listt(i+1 + 1); else tip1=listt(1); end if (i+k>=0) tipk=listt(i+k + 1); else tipk=listt(1); end if (i+k-1>=0) tipkm1=listt(i+k-1 + 1); else tipkm1=listt(1); end if k==1 if (ti<= t) && (t<tip1) val = 1 ; else val = 0 ; end return; else if (tipkm1 -ti) ~=0 val1= ((t- ti) / (tipkm1 -ti)) * B( i,k-1,t,listt); else val1= 0; end if (tipk - tip1)~=0 %version http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf val2= ((tipk - t) / (tipk - tip1)) * B( i+1,k-1,t,listt); %version http://www.inf.ed.ac.uk/teaching/courses/cg/d3/nonbspline.html %il y a une erreur! %val2= ((tipk - t) / (tipkm1 - ti)) * B( i+1,k-1,t,listt); %autre version foireuse en (4.7 de https://theses.lib.vt.edu/theses/available/etd-100699-171723/unrestricted/chapter4.PDF) %val2= ((tip1 - t) / (tipk - tip1)) * B( i+1,k-1,t,listt); else val2= 0; end val=val1+val2; return; end end
Résultat pour distribution uniforme et k=2
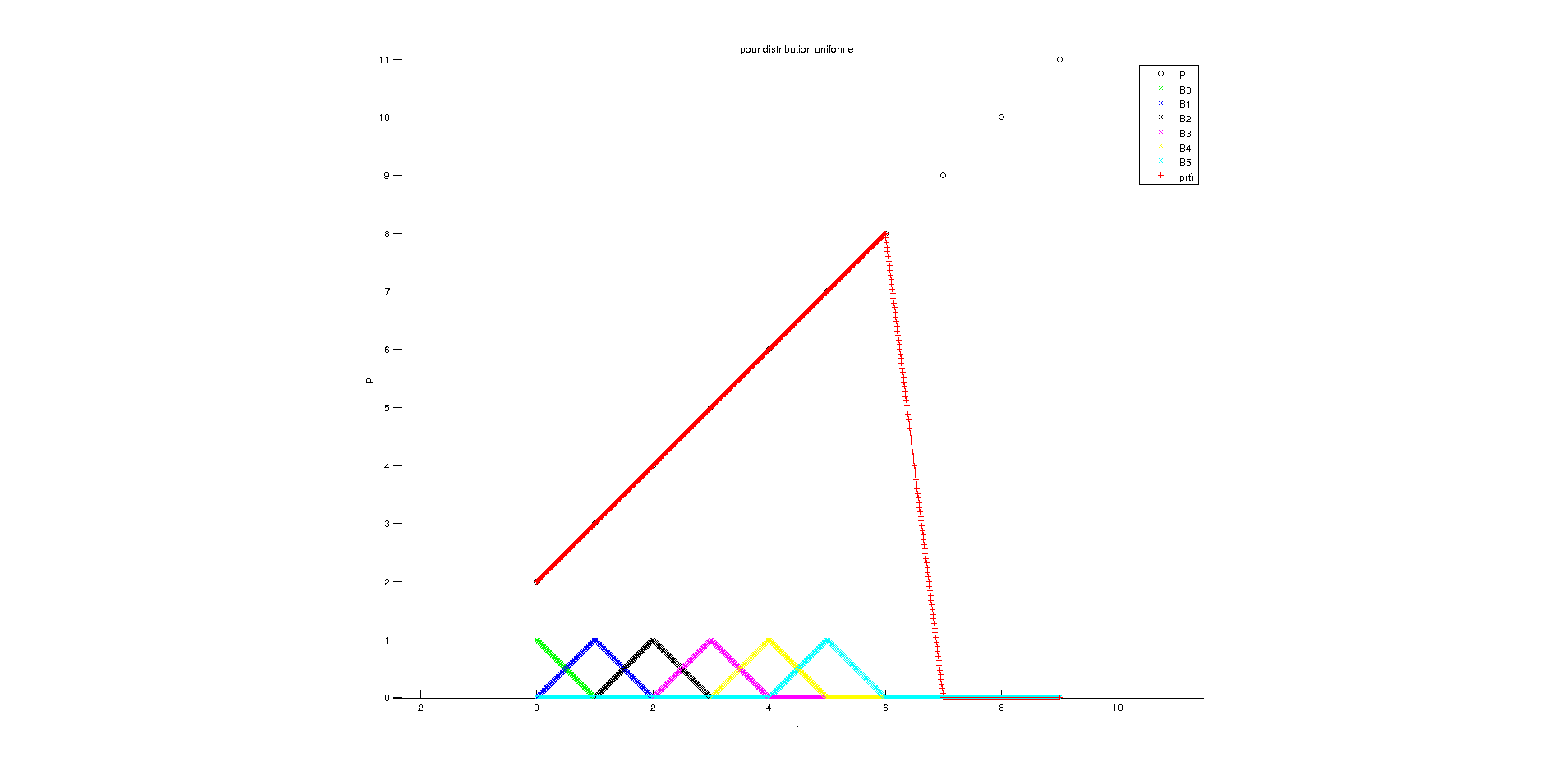
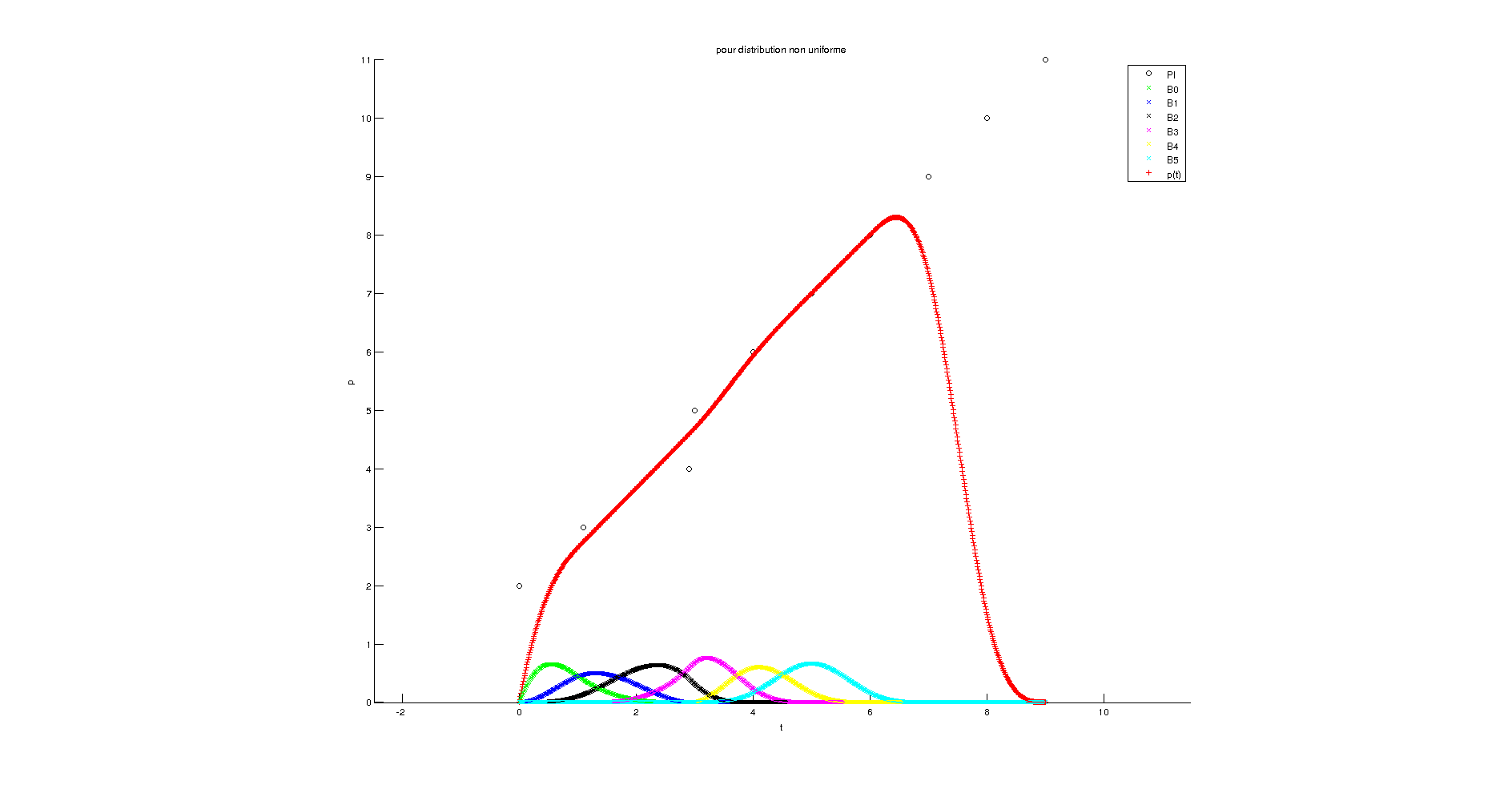
Résultat pour distribution non uniforme et k=2
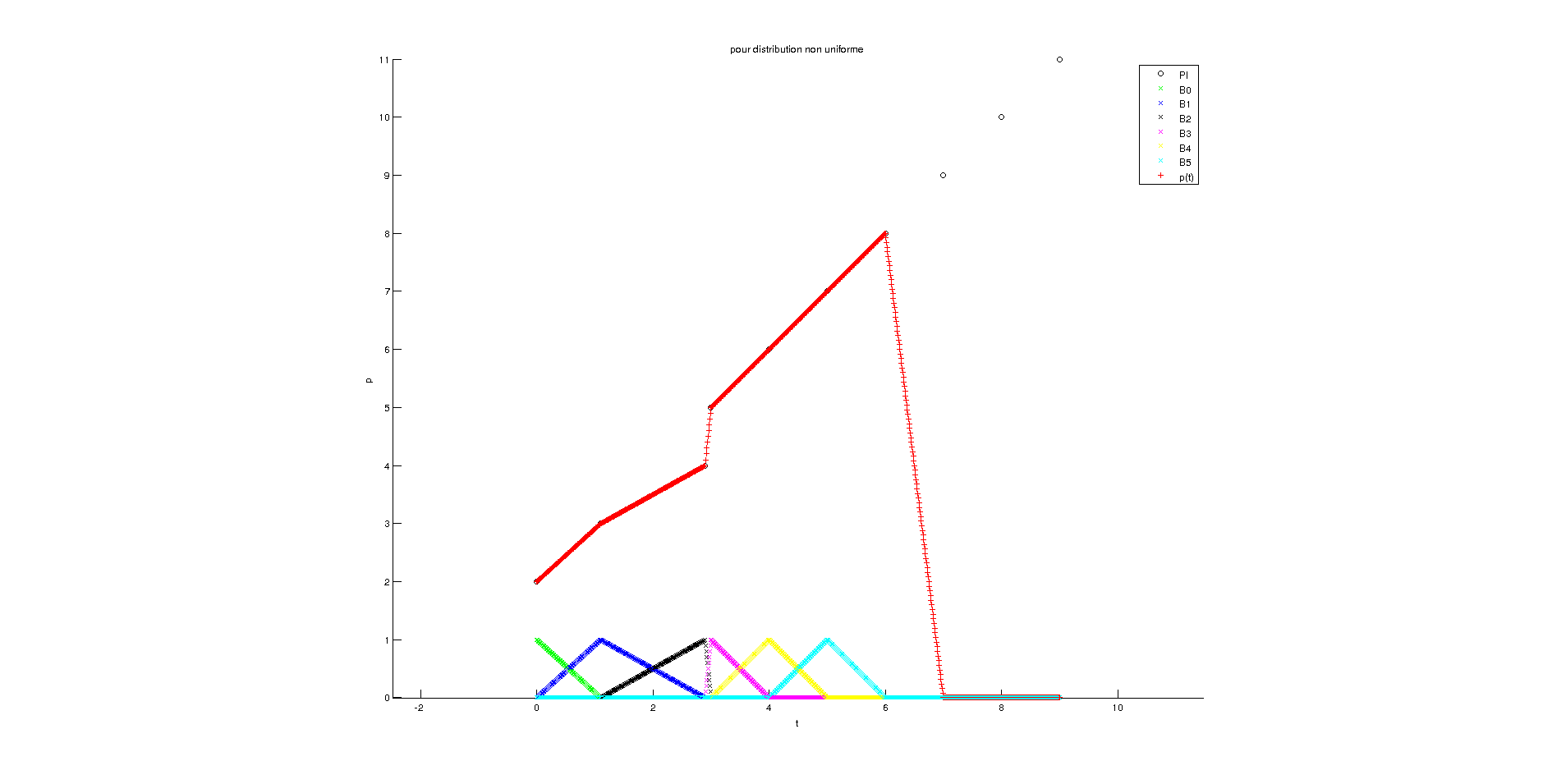
Résultat pour distribution uniforme et k=4
Résultat pour distribution non uniforme et k=4
Calcul des fonctions de base jusqu'à k=3 en considérant une distribution uniforme
Développement de l'équation de récurrence
Dernière étape du développement de l'équation de récurrence pour splines quadratiques
Script pour comparer les splines générées en utilisant l'équation de récurrence et les notations matricielles
- etudebaseu_non_cumulatif.m
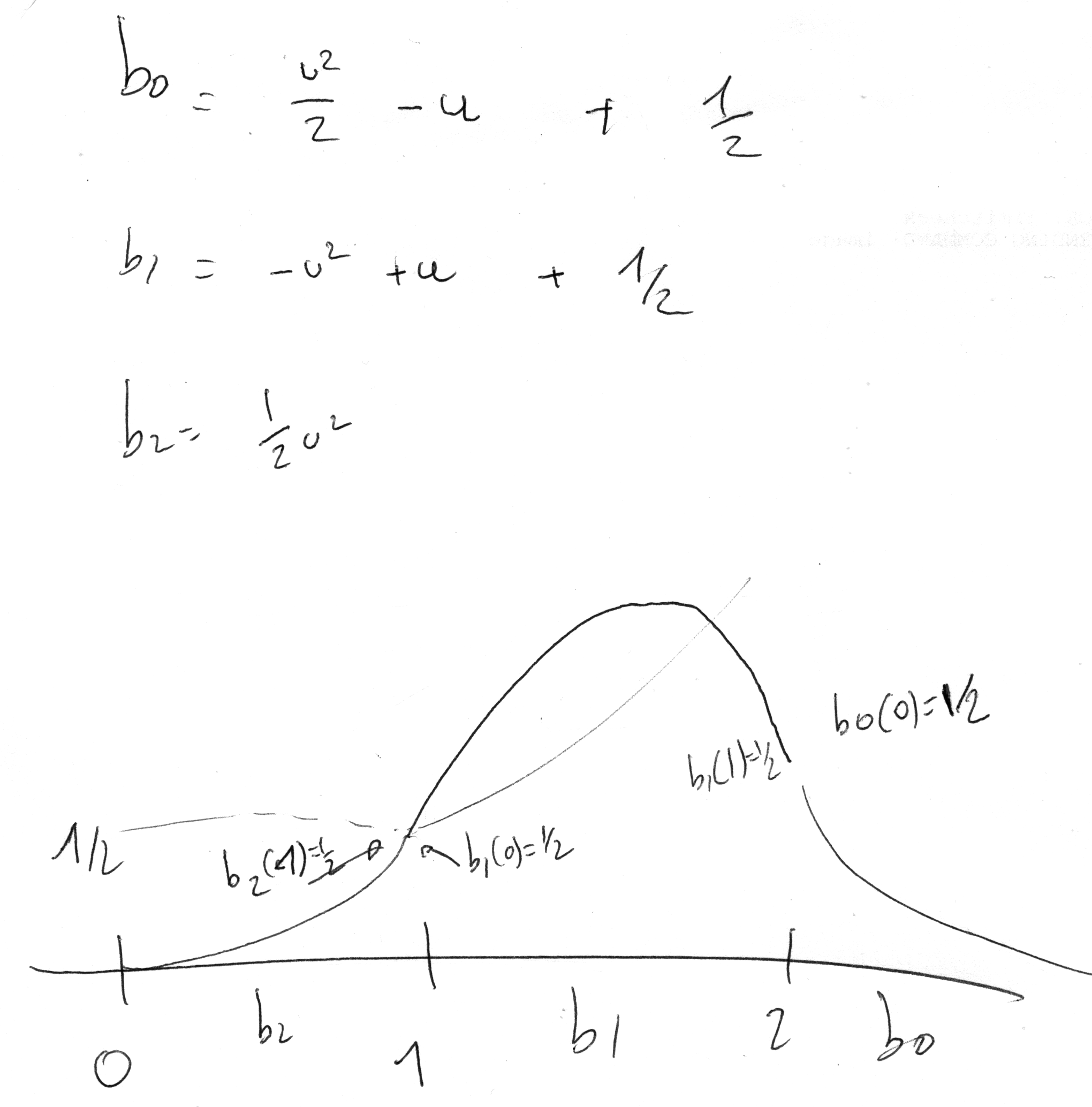
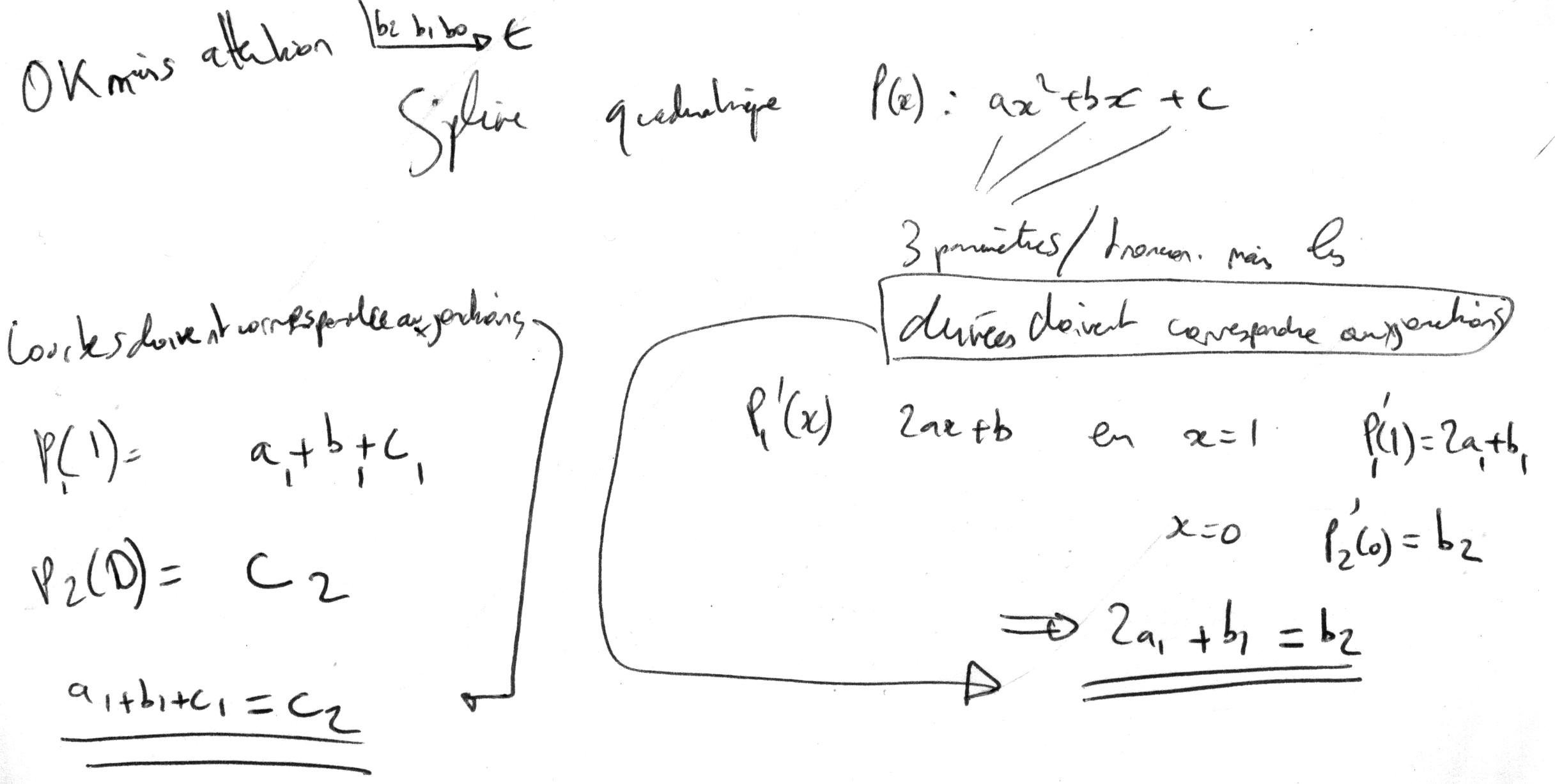
%B. Vandeportaele 2017 %étude du comportement des différentes fonctions de bases pour l'interpolation close all for ncurve=1:5 figure hold on tb=[]; for u=0:0.01:1 % b0=1; % b1=(u^3 -3*u^2 +3*u +5 )/6; % b2=(-2*u^3 +3*u^2 +3*u +1 )/6; % b3=(u^3 )/6; %à partir du papier de Huixian, matrice M3 exprimée en colone %spline de degré 3 if ncurve==1 b0=(-1*u^3 +3*u^2 -3*u +1 )/6; b1=(3*u^3 -6*u^2 +0*u +4 )/6; b2=(-3*u^3 +3*u^2 +3*u +1 )/6; b3=(u^3 )/6; elseif ncurve==2 b0=(-3*u^2 +6*u -3 )/6; b1=(9*u^2 -12*u +0 )/6; b2=(-9*u^2 +6*u +3 )/6; b3=(3*u^2 )/6; elseif ncurve==3 b0=(-6*u +6 )/6; b1=(18*u -12 )/6; b2=(-18*u +6 )/6; b3=(6*u )/6; elseif ncurve==4 % b0=(0.5 * u^2 ); % b1=(-u^2 +3*u -3/2 ); % b2=(0.5*u^2-3*u +9/2 ); % b3=0; % %Kaihuai M3 entre (8) et (9) % A B C b0=0.5*(1 - 2*u + 1 * u^2 ); % 1/2 -1 1/2 b1=0.5*(1 + 2*u + -2 * u^2 ); % -1 1 1/2 b2=0.5*( u^2 ); % 1/2 0 0 b3=0; elseif ncurve==5 %dérivée du cas précédent b0=0.5*(-2 + 2*u ); b1=0.5*(2 - 4*u ); b2=0.5*(2* u ); b3=0; end tb=[tb;u,b0,b1,b2,b3,b0+b1+b2+b3]; end plot (tb(:,1),tb(:,2),'r-'); plot (tb(:,1),tb(:,3),'g-'); plot (tb(:,1),tb(:,4),'b-'); plot (tb(:,1),tb(:,5),'k-'); plot (tb(:,1),tb(:,6),'c-'); %recolle les différentes fonctions de base pour illustrer le poids d'un %Omega pour u^ évoluant de 0 à 4 plot (tb(:,1)+1*ones(size(tb(:,1))),tb(:,4),'b-'); plot (tb(:,1)+2*ones(size(tb(:,1))),tb(:,3),'g-'); plot (tb(:,1)+3*ones(size(tb(:,1))),tb(:,2),'r-'); legend('b0','b1','b2','b3','somme'); end %retrouve l'expression polynomiale par morceau des Bi à partir de %l'expression récurente figure hold on axis equal % 2*b2=u^2 => b2=1/2 . u^2 %b2 est défini entre 0 et 1 donc pas de changement for u=0:0.01:1 plot (u,(1/2)*u^2,'b+'); end for u=1:0.01:2 plot (u,(1/2)*u*(2-u),'r+'); end for u=1:0.01:2 plot (u,(1/2)*(u-1)*(3-u),'g+'); end %2*b1 obtenu par somme de r+ et g+ %2*b1= (u*(2-u))+((u-1)*(3-u)) = 2u -u^2 + 3u -u^2 -3 +u = -2u^2 +6u -3 %b1= -u^2 +3u-3/2 for u=1:0.01:2 plot (u,(1/2)*((u*(2-u))+((u-1)*(3-u))),'y+'); end %ce b1 est défini entre 1 et 2 donc il faut faire un changement de variable %u'=(u+1) %b'1= -(u+1)^2 +3(u+1)-3/2 % -u^2 -1 -2u +3u +3 -3/2 % -u^2 +u +1/2 %affiche b'1 entre 0 et 1 for u=0:0.01:1 plot (u,( -u^2 +u +1/2),'yo'); end %2*b0 %2*b0=(3-u)*(3-u)=9+u^2-6u %b0= 1/2 u^2 -3u +9/2 for u=2:0.01:3 plot (u,(1/2)*(3-u)*(3-u),'k+'); end %ce b2 est défini entre 2 et 3 donc il faut faire un changement de variable %u'=(u+2) %b'2= 1/2 (u+2)^2 -3(u+2) +9/2 % = 1/2 (u^2 + 4 + 4u) -3u-6 +9/2 % = 1/2 u^2 + 2 + 2u -3u-6 +9/2 % = 1/2 u^2 -1u +1/2 %affiche 2*b'2 entre 0 et 1 for u=0:0.01:1 plot (u,((1/2)*u^2 -u +1/2),'ko'); end
NURBS
Attention les nurbs n'utilisent pas des fonctions de bases polynomiales mais des ratios…
extrait de https://fr.wikipedia.org/wiki/NURBS?veaction=edit
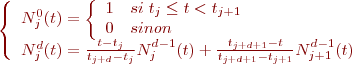
on s'intéresse à  :
:
Développement:
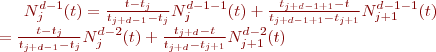
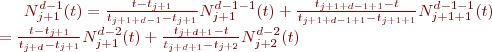
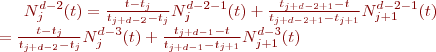
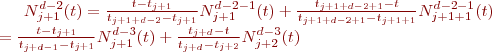
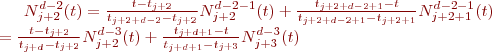
BSpline Non Uniforme
Développement des fonctions de base des BSpline non uniformes:
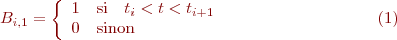
En utilisant cette définition, il est possible de calculer successivement les fonctions de base pour différents degrés en utilisant la formulation de récurrence de De Boor-Cox. Nous avons ainsi
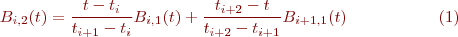
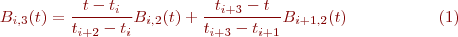
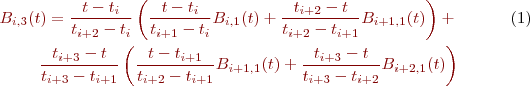
Après reformulation, on obtient:
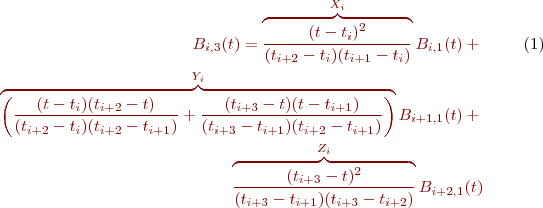
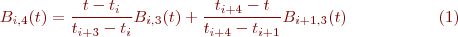
on peut développer la fonction de base pour k=4 tel que: