deflectometry
Table des matières
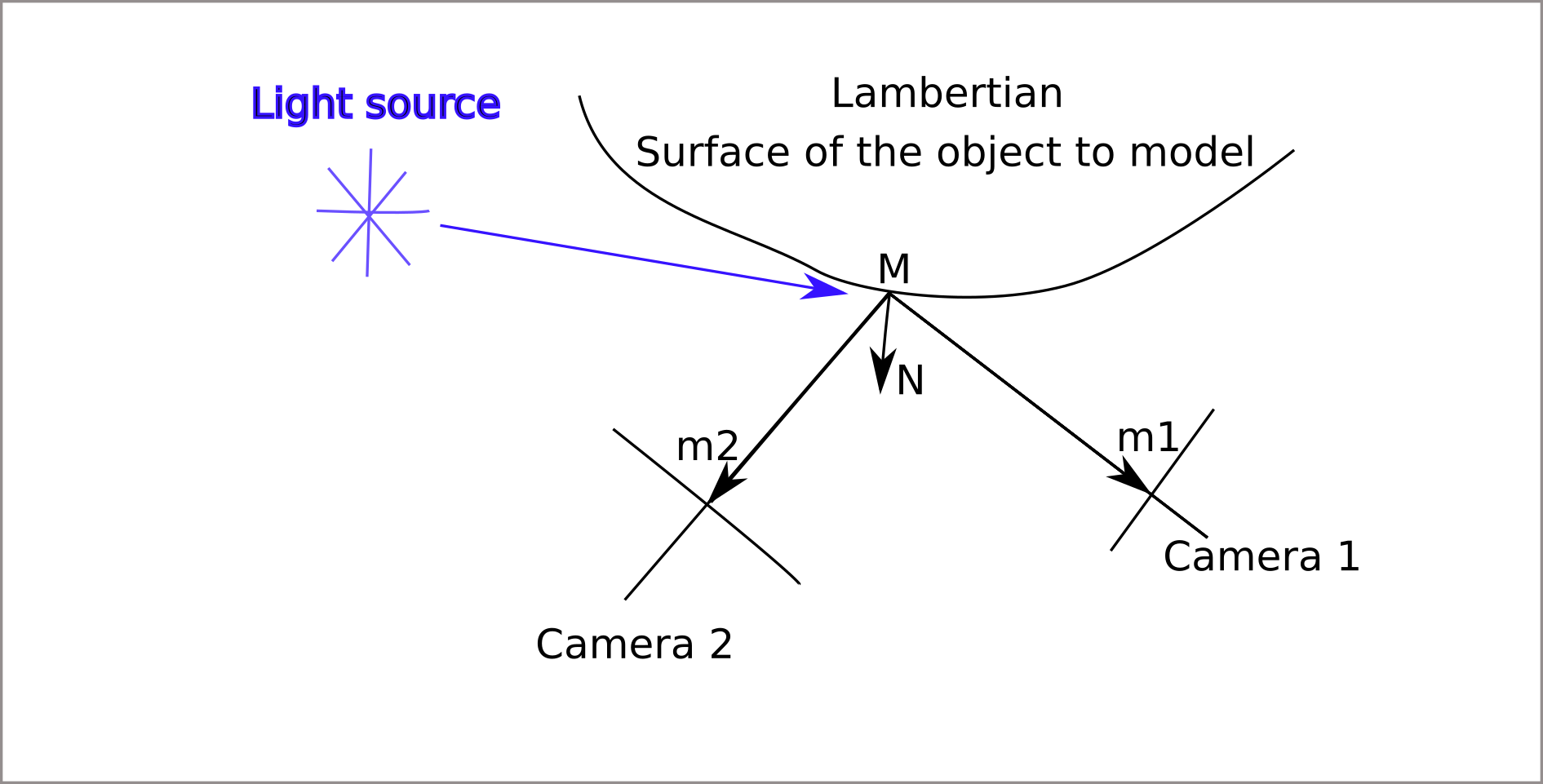
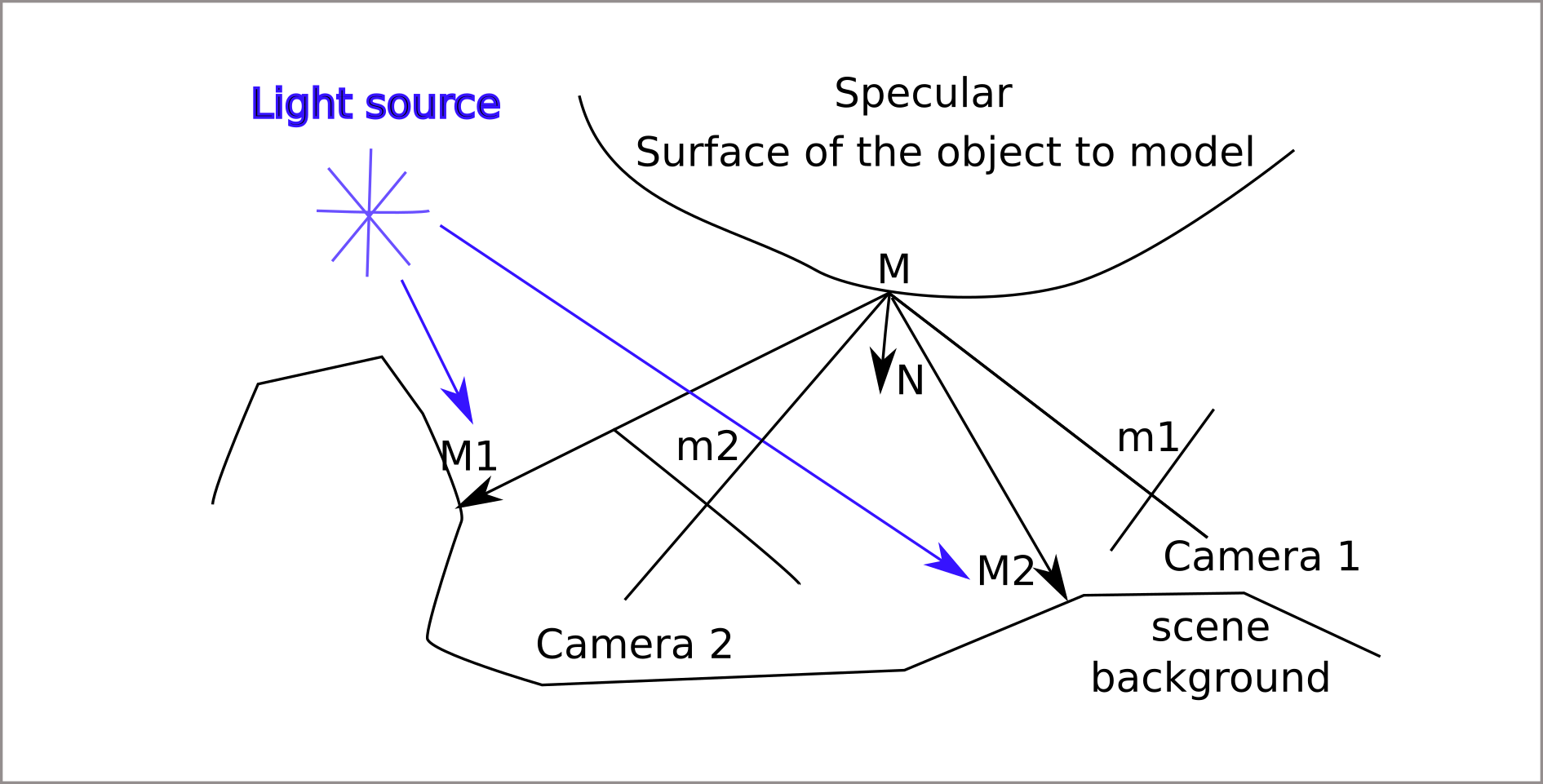
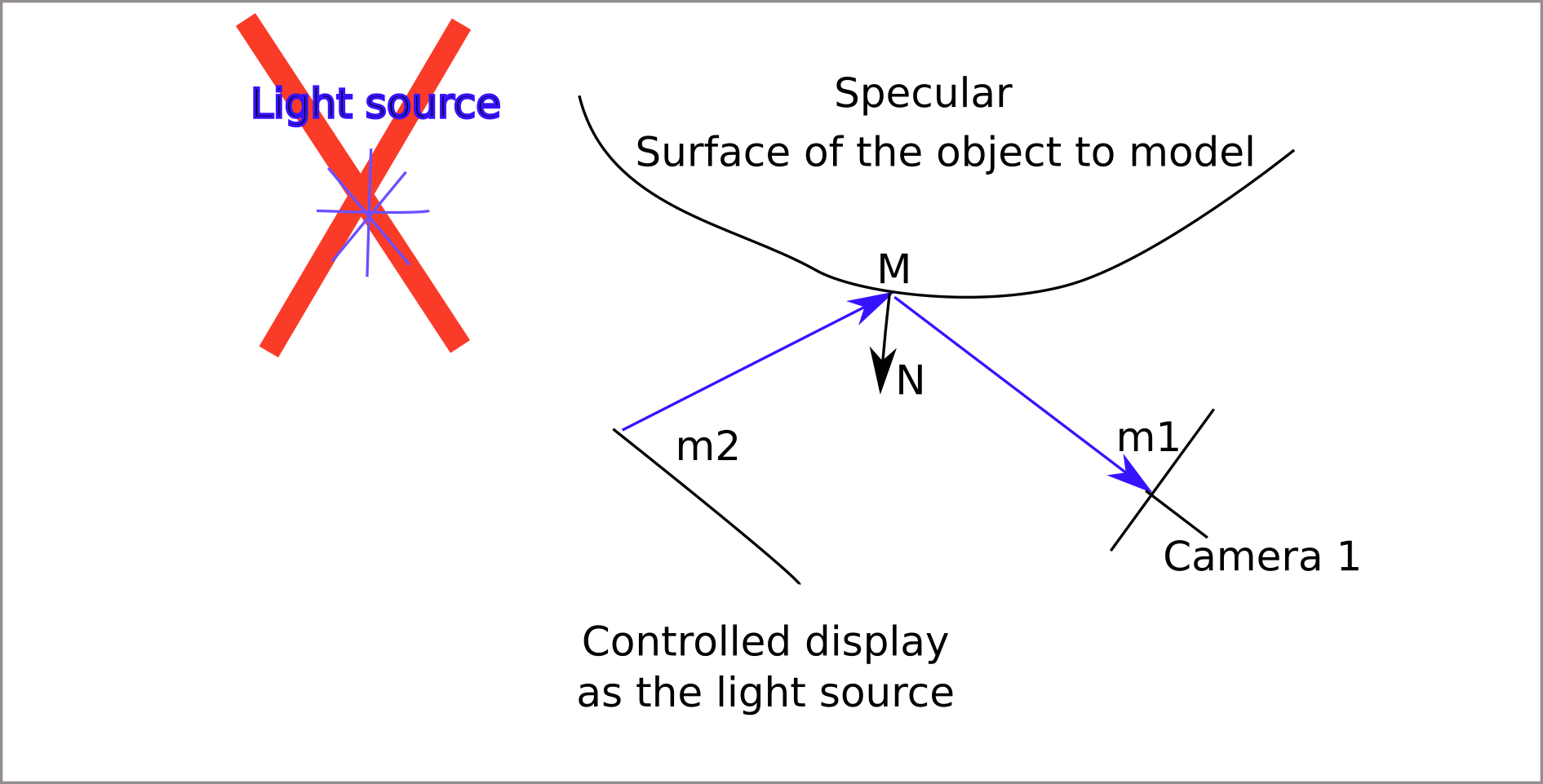
Deflectometry principle
svg file for the diagram: https://bvdp.inetdoc.net/files/deflectometry/graphique_pour_daniel/dessin8.svg
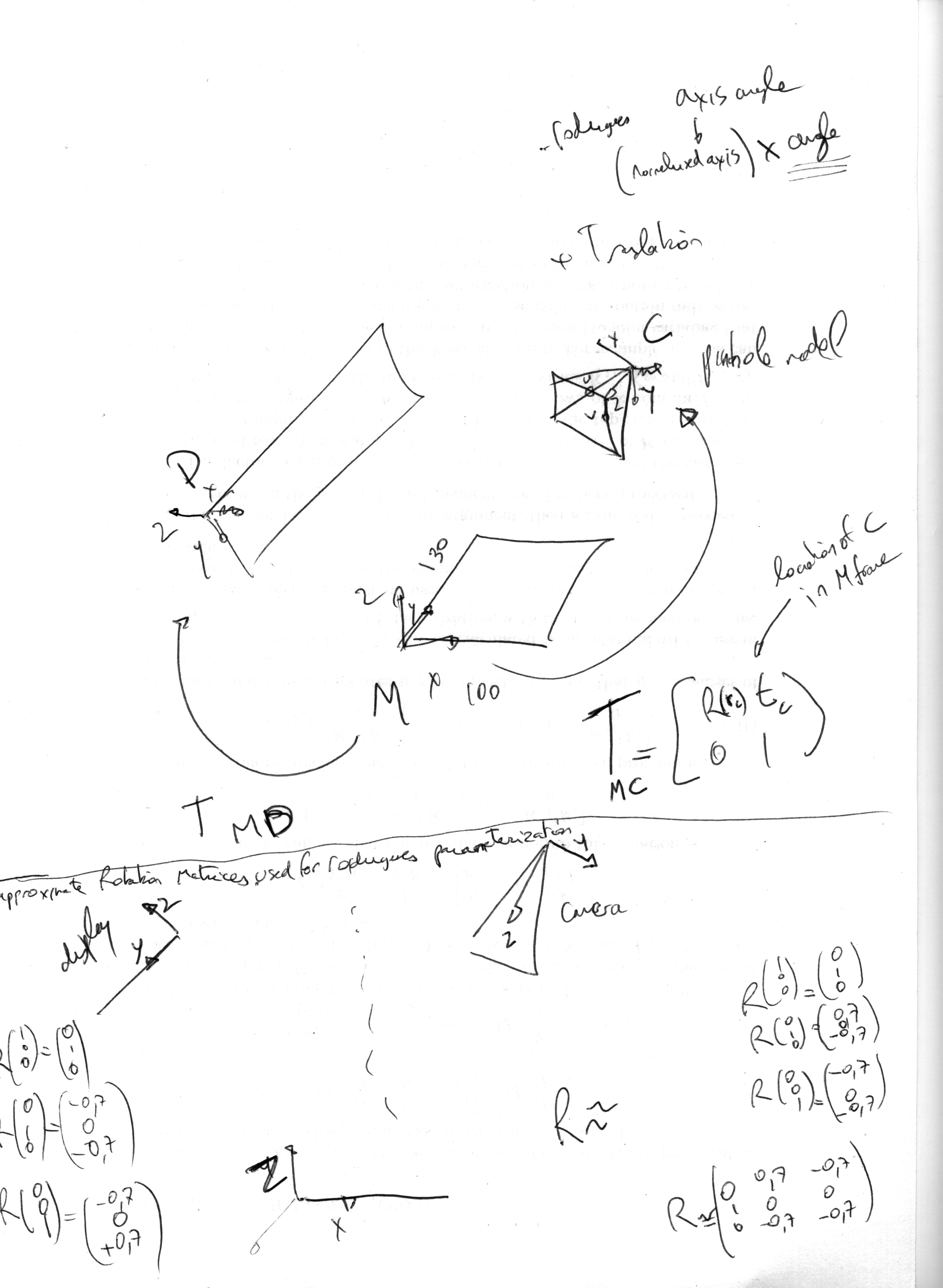
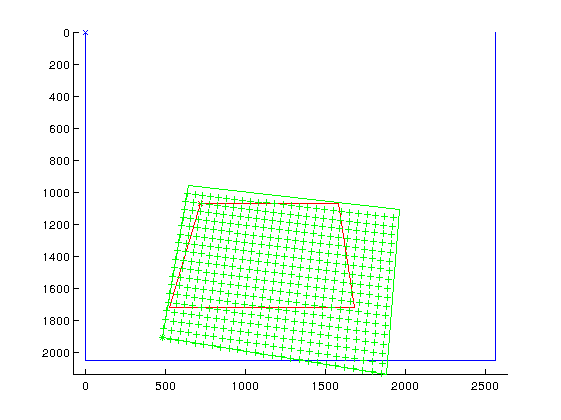
Deflectometry model simulator
- display_closed_contour.m
function display_closed_contour(countour,style,origin_style) if nargin==3 plot([countour(1,1)],[countour(1,2)],origin_style); end for n=1:size(countour,1)-1 plot([countour(n,1),countour(n+1,1)],[countour(n,2),countour(n+1,2)],style); end plot([countour(size(countour,1),1),countour(1,1)],[countour(size(countour,1),2),countour(1,2)],style); end
- rodrigues2R.m
function [ R] = rodrigues2R( wi ) %bvdp % R=rodrigues2R( [1, 2,-1]) %il faut que R*R^-1= Id et det(R)=1 theta=norm(wi,2) w=wi/theta ws=[0 -w(3) w(2) ; w(3) 0 -w(1) ; -w(2) w(1) 0] wwt=ws*ws if ~isa(w,'sym') & theta<eps % on ne peut pas tester theta en valeur si w est symbolique R=eye(3) else %cette formule ne fournit pas des matrices avec vecteurs de norme 1 %R=(cos(theta)*eye(3)) + ((1-cos(theta))*wwt) + (sin(theta)*ws) %la suivante est tirée de https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula R=eye(3) + (sin(theta)*ws) + ((1-cos(theta))*wwt) end end
- simu2.m
%B. Vandeportaële & D. Maestro 2017 close all clear all %symbolic or numeric simulation symbolic=1 %size of the mirror in x mirrorwidth=100; %size of the mirror in y mirrorheigth=130; if exist('symbolic','var') tcx=sym('tcx','real'); tcy=sym('tcy','real'); tcz=sym('tcz','real'); rcx=sym('rcx','real'); rcy=sym('rcy','real'); rcz=sym('rcz','real'); rc=[rcx,rcy,rcz]'; else tcx= 190; tcy= 85; tcz=200; %rc=[0,1,0]'*110*pi/180; %rc=[0,1,0]'*110*pi/180; %set the rotation matrix from axis correspondances Rapprox=[0 0.7 -0.7;1 0 0; 0,-0.7 -0.7]; det(Rapprox) [U,S,V] =svd(Rapprox) R=U*V' rr=rodrigues(R) rrangle=norm(rr) rraxis=rr/rrangle rc=rr end tc=[tcx,tcy,tcz]'; Tmc=[rodrigues2R(rc), tc; 0,0,0,1]; if exist('symbolic','var') fu=sym('fu','real'); fv=sym('fv','real'); pu=sym('pu','real'); pv=sym('pv','real'); else camera_image_width=2560; camera_image_height=2048; pu=camera_image_width/2; pv=camera_image_height/2; horizontal_fov=70*pi/180; vertical_fov=60*pi/180; fu=(camera_image_width/2)/tan(horizontal_fov/2); fv=(camera_image_height/2)/tan(vertical_fov/2); end K=[fu 0 pu 0; 0 fu pv 0; 0 0 1 0]; if ~exist('symbolic','var') mirror_corners=[0,0;mirrorwidth,0;mirrorwidth,mirrorheigth;0,mirrorheigth]; mirror_corners_projected=zeros(size(mirror_corners)); for n=1:size(mirror_corners,1) P=[ mirror_corners(n,:),0,1]'; PP=inv(Tmc)*P if (PP(3)<0) display('the point is behind the camera'); end p=K*PP; p=p/p(3); mirror_corners_projected(n,:)=p(1:2)'; end end if exist('symbolic','var') display_pixel_size_x=sym('display_pixel_size_x','real'); display_pixel_size_y=sym('display_pixel_size_y','real'); else camera_image_boundaries=[0,0;camera_image_width,0;camera_image_width,camera_image_height;0,camera_image_height]; display_pixel_size_x=0.205; display_pixel_size_y=0.205; display_pixel_width=2560; display_pixel_height=1800; %metric unit mm display_metric_width=display_pixel_size_x*display_pixel_size_x; display_metric_height=display_pixel_size_y*display_pixel_size_y; end pixel2metric=[display_pixel_size_x 0 0; 0 display_pixel_size_y 0; 0 0 1]; if exist('symbolic','var') tdx=sym('tdx','real'); tdy=sym('tdy','real'); tdz=sym('tdz','real'); rdx=sym('rdx','real'); rdy=sym('rdy','real'); rdz=sym('rdz','real'); rd=[rcx,rcy,rcz]'; else %set the rotation matrix from axis correspondances %close to perfect configuration %Rapprox2=[0 -0.7 -0.7;1 0 0; 0,-0.7 +0.7]; %another configuration with 3 degrees of freedom rotation Rapprox2=[0 -0.7 -0.5;0.7 0.2 0.1; 0,-0.7 +0.9]; [U,S,V] =svd(Rapprox2); R2=U*V'; rr2=rodrigues(R2); rrangle2=norm(rr2); rraxis2=rr2/rrangle2; rd=rr2 tdx=-64; tdy=-220; tdz=530; end % rd=[rdx,rdy,rdz]'; td=[tdx,tdy,tdz]'; Tmd=[rodrigues2R(rd), td; 0,0,0,1]; %Tdm=inv(Tmd); Treflection=[1 0 0 0; 0 1 0 0 ; 0 0 -1 0; 0 0 0 1]; MMM=[1 0 0; 0 1 0; 0 0 0; 0 0 1]; %form P2 to P3 in z=0 plane if ~exist('symbolic','var') display_image_boundaries=[0,0;display_pixel_width,0;display_pixel_width,display_pixel_height;0,display_pixel_height]; display_corners_projected=zeros(size(display_image_boundaries)); for n=1:size(mirror_corners,1) Pd=[ display_image_boundaries(n,:),1]' Pdmetric=pixel2metric*Pd; %PdmetricP3=[Pdmetric(1:2);0;Pdmetric(3)]; %compute location in P3 for z=0 plane PdmetricP3=MMM*Pdmetric; P=Treflection*Tmd*PdmetricP3; PP=inv(Tmc)*P if (PP(3)<0) display('the point is behind the camera'); end p=K*PP; p=p/p(3); display_corners_projected(n,:)=p(1:2)'; end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %computation of the homography between display and camera taking %into account the reflexion Hcd=K*inv(Tmc)*Treflection*Tmd*MMM*pixel2metric %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% if exist('symbolic','var') jacobian(reshape(Hcd,9,1),[rd]) end if exist('symbolic','var') jacobian(reshape(Tmd,16,1),[rd]) end if exist('symbolic','var') %what happen if we use Tcm instead of Tmc=> other parameterization tcix=sym('tcix','real'); tciy=sym('tciy','real'); tciz=sym('tciz','real'); rcix=sym('rcix','real'); rciy=sym('rciy','real'); rciz=sym('rciz','real'); rci=[rcix,rciy,rciz]'; tci=[tcix,tciy,tciz]'; Tcm=[rodrigues2R(rci), tci; 0,0,0,1]; Hcd=K*Tcm*Treflection*Tmd*MMM*pixel2metric J= jacobian(reshape(Hcd,9,1),[rd',td',rci',tci']) end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %display %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% if ~exist('symbolic','var') figure hold on axis equal axis ij display_closed_contour(camera_image_boundaries,'b-','bx') display_closed_contour(mirror_corners_projected,'r-','rx') display_closed_contour(display_corners_projected,'g-','gx') for ud=0:100:display_pixel_width-1 for vd=0:100:display_pixel_height-1 p=Hcd*[ud;vd;1]; p=p/p(3); plot(p(1),p(2),'g+'); end end end
2D analysis for uncertainty propagation
- simu2D.m
%B. Vandeportaële & D. Maestro 2017 close all clear all %example for the inversion of P1 to P1 scale and offset pixperm=sym('pixperm','real'); pud=sym('pud','real'); Kd=[pixperm pud; 0 1] a=sym('a','real'); b=sym('b','real'); c=sym('c','real'); d=sym('d','real'); Kdinv=[a b;c d ] eqn= reshape(Kdinv*Kd-eye(2),4,1) S=solve(eqn,a,b,c,d) Kdinv=[S.a S.b;S.c S.d] jacobian(reshape(Kdinv,4,1),[pixperm,pud]) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tcx=sym('tcx','real'); tcy=sym('tcy','real'); r11=sym('r11','real'); r12=sym('r12','real'); r21=sym('r21','real'); r22=sym('r22','real'); M=[r11,r12,tcx;r21,r22,tcy ;0 0 1] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% fuc=sym('fuc','real'); puc=sym('puc','real'); K=[fuc puc 0; 0 1 0]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% E=[1 0;0 0 ;0 1] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% H=K*M*E*Kdinv %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tdx=sym('tdx','real'); tdy=sym('tdy','real'); thetad=sym('thetad','real'); Md=[cos(thetad),-sin(thetad), tdx;sin(thetad),cos(thetad),tdy; 0, 0, 1] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Fitting of sinus function
- phase.m
%@Bertrand Vandeportaele LAAS 2017 function phasefunc() close all symbolicComputation=false; ud=218; vd=153; ud=289; vd=93; of=100; af=73; freq=6/(1920); wt=2*pi*freq; lum=[]; lumn=[]; n=[]; nbPointsPerPeriod=400 global gnoiseLevel gnoiseLevel=3 %useSyntheticData=true useSyntheticData=false if useSyntheticData %polynomial for some non linear disturbance pol=[ 0.003; 0.35; 10] %polynomial for some no disturbance %pol=[ 0; 1; 0] for i=1:nbPoints*PerPeriod p=i*2*pi/nbPointsPerPeriod; deltai=ud*wt; l=of+af*sin(deltai+p); lum=[lum,l]; %non linear disturbance l2=pol(3)+pol(2)*l+pol(1)*l^2; %add noise ln=l2+gnoiseLevel*randn(1); lumn=[lumn,ln]; n=[n,i-1]; end else folder_path = './pos_02/0016/H/'; %folder_path = './pos_02/0032/H/'; %folder_path = './pos_02/0064/H/'; %file_extension='bmp'; %num_imgs= 11 folder_path = '/media/HD500GO/daniel/phases/gray/m_00/t4096/pos_02/0016/H/' file_extension='tif'; num_imgs= 64 ud=128; vd=1024; % vd=1 folder_path = '/media/HD500GO/daniel/phases/gray/m_00/t40/m_00/pos_02/0040/H/' file_extension='tif'; num_imgs= 128 ud=1280; vd=1024; vd=1000 vd=400 %To avoid reloading the images each time. % clear I to force it global I %if true if (size(I,1)==0) || (size(I,2)==0) %% Load Images fprintf('Start loading data\n') tic; for indx=0:num_imgs-1 ima_name = sprintf('%s%s%03d.%s', folder_path,'img_',indx,file_extension); if indx==0 I0 = imread(ima_name); [ rs, cs] = size(I0); % Allocate matrix I = zeros(rs, cs, num_imgs); I(:,:,1) = I0; else %ima_name = fullfile(folder_path, image_files(indx).name); I(:,:,indx+1) = imread(ima_name); end end fprintf([num2str(num_imgs), ' Images Loaded. ']) toc end end n=(0:num_imgs-1)'; lumn=reshape(I(vd,ud,:),num_imgs,1)'; lum=lumn; nbPointsPerPeriod=num_imgs %polynomial for no disturbance pol=[ 0; 1; 0] %numberOfSamplesForMeaning=10 %mask=(1/numberOfSamplesForMeaning)*ones(1,numberOfSamplesForMeaning) %lumn=conv(lumn,mask,'same') global gpuls gpuls=2*pi/nbPointsPerPeriod; %%%%%%%%%%%%%%%%TEST to reduce the number of input data%%%%%%%%%%%%%%%%%%%% % nbPointsPerPeriod=6 % n=n(1:nbPointsPerPeriod) % lum=lum(1:nbPointsPerPeriod) % lumn=lumn(1:nbPointsPerPeriod) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%TEST pertubate some points to check the robustness %lumn(40)=6000 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tic [xLinear covarianceOutLinear]=fitSinusLinear(n,lumn,gpuls) toc tic [xLinearOpt covarianceOutLinearOpt,err]=fitSinusLinearOptimized(n,lumn,gpuls) toc [xPerfect covarianceOutPerfect]=fitSinusLinear(n,lum,gpuls) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %non linear method if symbolicComputation ofs = sym('ofs','real'); amp = sym('amp','real'); gpuls = sym('puls','real'); phas = sym('phas','real'); t = sym('t','real'); y=ofs+amp*sin(gpuls*t+phas) ymes = sym('ymes','real'); res=expand((ymes-y)) %jacobian of res used during optimization J=jacobian(res,[ofs,amp,phas])' %jacobian of res^2, should be 0 at the end of the optimization only %when there is no noise on the data %J2=jacobian(res^2,[ofs,amp,phas])' end %ofs=of+10; %amp=af*0.9; %phas=0; %x0=[ofs,amp,phas]; %x0=x0+[10,40,0.3]%add some error [xNonLinear,resxNonLinear,JxNonLinear]= sinusNonLinearFit(n,lumn,xLinear); %NON!!!!!!!!!!!!!!!!! %covarianceInNonLinear=diag(resxNonLinear.*resxNonLinear); %W=inv(covarianceInNonLinear); %mean of absolute value of errr mean (abs(resxNonLinear),1) variance=var(resxNonLinear) standardDeviation=variance^0.5 W=eye(size(resxNonLinear,1))*variance^-1; JxNonLinear InformationOutNonLinear= (JxNonLinear'*W*JxNonLinear) covarianceOutNonLinear= inv(InformationOutNonLinear); displayResult(xLinear, covarianceOutLinear,'xLinear ' ) %theese 2 values have comparable variances displayResult(xNonLinear, covarianceOutNonLinear,'xNonLinear ' ) %return %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %non linear method taking into account the non linearity of the %camera/display if symbolicComputation ofs = sym('ofs','real'); amp = sym('amp','real'); gpuls = sym('puls','real'); phas = sym('phas','real'); t = sym('t','real'); yperfect=ofs+amp*sin(gpuls*t+phas); nla = sym('nla','real'); nlb = sym('nlb','real'); nlc = sym('nlc','real'); y=nla * yperfect^2 + nlb * yperfect + nlc; ymes = sym('ymes','real'); res=expand((ymes-y)) %jacobian of res used during optimization J=jacobian(res,[ofs,amp,phas,nla,nlb,nlc])' end %ofs=of+10; %amp=af*0.9; %phas=0; %x0=[ofs,amp,phas]; %x0=x0+[10,40,0.3]%add some error x0_2=[xLinear, 0, 1, 0] %x0_2=[1500 1.3 0.5 , 0, 1, 0] [xNonLinear_2,resxNonLinear_2,JxNonLinear_2]= sinusNonLinearFit2(n,lumn,x0_2) %covarianceOutNonLinear_2=zeros(6,6); %covarianceOutNonLinear_2=JxNonLinear_2'*diag(resxNonLinear_2.*resxNonLinear_2)*JxNonLinear_2 %TODO: plot that non linear function and generate the corrected plot %for sinus! %JxNonLinear_2(:,4)=0 pol=xNonLinear_2(4:6) %!!!!! NON j'ai estimé le polynome inverse!!!! %xNonLinear_2=xNonLinear_2(1:3); %covarianceOutNonLinear_2=JxNonLinear_2(:,1:3)'*diag(resxNonLinear_2.*resxNonLinear_2)*JxNonLinear_2(:,1:3) %xNonLinear_2(4:6) =pol %covarianceOutNonLinear_2(6,6)=0 %W=diag(resxNonLinear_2.*resxNonLinear_2); %covarianceInNonLinear=inv(W) %covarianceInNonLinear=eye(128); %InformationOutNonLinear_2= (JxNonLinear_2'*covarianceInNonLinear*JxNonLinear_2) %covarianceOutNonLinear_2= inv(InformationOutNonLinear_2) resxNonLinear_2 %mean of absolute value of errr mean (abs(resxNonLinear_2),1) variance=var(resxNonLinear_2) variancebis=mean(resxNonLinear_2.*resxNonLinear_2) %>give approximately the variance if the mean is close to 0 (no bias) varianceter=(resxNonLinear_2'*resxNonLinear_2)/nbPointsPerPeriod standardDeviation=variance^0.5 % W1=eye(size(resxNonLinear_2,1))*variance^-1; %W2=diag( ((resxNonLinear_2.*resxNonLinear_2)*nbPointsPerPeriod).^-1 ) %W2=diag( ((resxNonLinear_2.^2)*nbPointsPerPeriod).^-1 ) %the squared error is computed for each data point, with a sample size of %one, so the variance of this 1 set is equal o val^2/1 %W2=diag( ((resxNonLinear_2.^2)).^-1 ); %<==> W2=diag( (resxNonLinear_2.^-2)) %traceW1=trace(W1) %MtraceW2=trace(W2) %return %[diag(W1),diag(W2)]'*ones(128,2) %return W=W1; %processing of uncertainty using the whole set of parameters lead to %non invertible information matrix InformationOutNonLinear_2= (JxNonLinear_2'*W*JxNonLinear_2) covarianceOutNonLinear_2= inv(InformationOutNonLinear_2) %= InformationOutNonLinear_2^-1 [u,s,v]=svd(covarianceOutNonLinear_2) covarianceOutNonLinear_2-( u*s*v') sinv=zeros(6,6); for i=1:6 s(i,i) %The sixth term is e-13 and the first is e+16, poor conditionning if (i~=6) sinv(i,i)=1/s(i,i); end end %sinv=inv(s) sinv inverse=v*sinv*u' for i=1:6 inverse(i,i) end rank(covarianceOutNonLinear_2) inverse*covarianceOutNonLinear_2 if false end %work on a reduced version focucing on the sinusoidal function parameters, %because the information matrix is of rank 3 only! JxNonLinear_2red=JxNonLinear_2(:,1:3); InformationOutNonLinear_2= (JxNonLinear_2red'*W*JxNonLinear_2red) rank(InformationOutNonLinear_2) covarianceOutNonLinear_2= inv(InformationOutNonLinear_2) covarianceOutNonLinear_2(1,1) covarianceOutNonLinear_2(2,2) covarianceOutNonLinear_2(3,3) %add 0s to the covariance matrix so it can be displayed later covarianceOutNonLinear_2(6,6)=0; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% figure subplot(1,3,1); %xx=1:255; xx=1:(2^12)-1; yy=polyval(pol,xx); plot(xx, yy,'r-') subplot(1,3,2); hold on plot(n, lum,'r+') displaySin(min(n)-1,max(n)+1,xPerfect,'r-'); plot(n, lumn,'b+') displaySin(min(n)-1,max(n)+1,xLinear,'k:'); displaySin(min(n)-1,max(n)+1,xNonLinear,'g--'); displaySinNonLinear(min(n)-1,max(n)+1,xNonLinear_2,'b--'); legend('data without noise','function without noise','data with noise','fitted function using linear method','fitted function using non linear method','fitted function using non linear method and non linear correction') subplot(1,3,3); %resxNonLinear=randn(size(resxNonLinear,1),1); resToPlot=resxNonLinear_2; numberOfBinsToPlot=12; maxErr=round(max(abs(resToPlot)))+1; binranges = [-maxErr:maxErr/(numberOfBinsToPlot-2):maxErr]; %binranges = [-maxErr:maxErr/10:maxErr]; nbBins=size(binranges,1); [nelements,ind] =histc(resToPlot,binranges); plot(binranges,nelements*nbBins/nbPointsPerPeriod,'r+'); hold on plot(resToPlot,zeros(size(resToPlot,1)),'g+'); meanOfError=mean(resToPlot) varianceOfError=var(resToPlot) standardDeviationOfError=sqrt(varianceOfError) gaussianSamplesx=[-maxErr:0.1:maxErr]; gaussianSamplesy=(1/sqrt(2*pi*varianceOfError))*exp(-( ((gaussianSamplesx-meanOfError).^2)/(2*varianceOfError))); plot(gaussianSamplesx, gaussianSamplesy ,'b-'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% displayResult(xPerfect, covarianceOutPerfect,'xPerfect ' ) displayResult(xLinear, covarianceOutLinear,'xLinear ' ) displayResult(xNonLinear_2, covarianceOutNonLinear_2,'xNonLinear_2 ' ) %convert the 3sigma uncertainty in phase to pixel position pixelPeriod=16 phase3sigma=3*sqrt(covarianceOutLinear(3,3)) pixelLocation3Sigma=phase3sigma*pixelPeriod/(2*pi) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %compare the distribution of the error with the theroretic one using the %Cumulative distribution function figure resxNonLinear_2sorted=sort(resxNonLinear_2); plot(resxNonLinear_2sorted,n/nbPointsPerPeriod,'r-'); %fonction de répartition: https://en.wikipedia.org/wiki/Normal_distribution variance=var(resxNonLinear_2sorted); x=[-5*sqrt(variance):5*sqrt(variance)]'; for i=1:size(x,1) y(i)=(1/2)*(1+erf( (x(i)-mean(resxNonLinear_2sorted))/(sqrt(variance)*sqrt(2)))); end hold on plot(x,y,'b-'); legend('observed','ideal') title('Cumulative distribution function') end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [x,resx,Jx]= sinusNonLinearFit(datax,datay,x0) global gdatax global gdatay gdatax=datax; gdatay=datay; [res0] = myfun2(x0); options = optimset('Jacobian','on','Display','iter', 'MaxFunEvals',200, 'Algorithm' ,{'levenberg-marquardt',.005}); [x,resnorm,residual,exitflag] = lsqnonlin(@myfun2,x0,-Inf,+Inf,options); % Invoke optimizer %[resxPerfect] = myfun2(xPerfect); %norm(resxPerfect,2) [resx,Jx] = myfun2(x); norm(resx,2) end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [res,J] = myfun2(x) global gpuls global gdatax global gdatay ofs=x(1); amp=x(2); phas=x(3); nbdata=max(size(gdatax)); res=zeros(nbdata,1); J=zeros(nbdata,3); %J2=zeros(nbdata,3); for i=1:nbdata t=gdatax(i); ymes=gdatay(i); y=ofs+amp*sin(gpuls*t+phas); res(i)=ymes-y; %jacobian for residuals J(i,:)=[ -1, - cos(gpuls*t)*sin(phas) - sin(gpuls*t)*cos(phas), amp*sin(gpuls*t)*sin(phas) - amp*cos(gpuls*t)*cos(phas)]; %jacobian for residuals^2 %J2(i,:)=[ 2*ofs - 2*ymes + 2*amp*cos(puls*t)*sin(phas) + 2*amp*sin(puls*t)*cos(phas), % 2*(cos(puls*t)*sin(phas) + sin(puls*t)*cos(phas))*(ofs - ymes + amp*cos(puls*t)*sin(phas) + amp*sin(puls*t)*cos(phas)), % 2*(amp*cos(puls*t)*cos(phas) - amp*sin(puls*t)*sin(phas))*(ofs - ymes + amp*cos(puls*t)*sin(phas) + amp*sin(puls*t)*cos(phas))]; end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [res] = displaySin(tmin,tmax,x,style) global gpuls ofs=x(1); amp=x(2); phas=x(3); t=tmin:0.1:tmax; recons=ofs+amp*sin(gpuls.*t+phas); plot(t,recons,style) end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [x,resx,Jx]= sinusNonLinearFit2(datax,datay,x0) global gdatax global gdatay gdatax=datax; gdatay=datay; %[res0] = myfun3(x0); options = optimset('Jacobian','on','Display','iter', 'MaxFunEvals',200, 'Algorithm' ,{'levenberg-marquardt',.005}); %options = optimset('Jacobian','off','Display','iter', 'MaxFunEvals',200, 'Algorithm' ,{'levenberg-marquardt',.005}); [x,resnorm,resx,exitflag,output,lambda,Jx] = lsqnonlin(@myfun3,x0,-Inf,+Inf,options); % Invoke optimizer %perturbate to add bias %resx=resx+100*ones(size(resx,2)); %[resxPerfect] = myfun2(xPerfect); %norm(resxPerfect,2) %[resx,Jx] = myfun3(x); norm(resx,2) end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [res,J] = myfun3(x) global gpuls global gdatax global gdatay ofs=x(1); amp=x(2); phas=x(3); nla=x(4); nlb=x(5); nlc=x(6); nbdata=max(size(gdatax)); res=zeros(nbdata,1); J=zeros(nbdata,6); %J2=zeros(nbdata,3); for i=1:nbdata t=gdatax(i); ymes=gdatay(i); yperfect=ofs+amp*sin(gpuls*t+phas); y=nla * yperfect^2 + nlb * yperfect + nlc; res(i)=ymes-y; %jacobian for residuals J(i,:)=[ - nlb - 2*nla*ofs - 2*amp*nla*cos(gpuls*t)*sin(phas) - 2*amp*nla*sin(gpuls*t)*cos(phas) - nlb*cos(gpuls*t)*sin(phas) - nlb*sin(gpuls*t)*cos(phas) - 2*amp*nla*cos(gpuls*t)^2*sin(phas)^2 - 2*amp*nla*sin(gpuls*t)^2*cos(phas)^2 - 2*nla*ofs*cos(gpuls*t)*sin(phas) - 2*nla*ofs*sin(gpuls*t)*cos(phas) - 4*amp*nla*cos(gpuls*t)*sin(gpuls*t)*cos(phas)*sin(phas) amp*nlb*sin(gpuls*t)*sin(phas) - amp*nlb*cos(gpuls*t)*cos(phas) - 2*amp*nla*ofs*cos(gpuls*t)*cos(phas) - 2*amp^2*nla*cos(gpuls*t)*sin(gpuls*t)*cos(phas)^2 + 2*amp^2*nla*cos(gpuls*t)*sin(gpuls*t)*sin(phas)^2 + 2*amp*nla*ofs*sin(gpuls*t)*sin(phas) - 2*amp^2*nla*cos(gpuls*t)^2*cos(phas)*sin(phas) + 2*amp^2*nla*sin(gpuls*t)^2*cos(phas)*sin(phas) - ofs^2 - amp^2*cos(gpuls*t)^2*sin(phas)^2 - amp^2*sin(gpuls*t)^2*cos(phas)^2 - 2*amp*ofs*cos(gpuls*t)*sin(phas) - 2*amp*ofs*sin(gpuls*t)*cos(phas) - 2*amp^2*cos(gpuls*t)*sin(gpuls*t)*cos(phas)*sin(phas) - ofs - amp*cos(gpuls*t)*sin(phas) - amp*sin(gpuls*t)*cos(phas) -1]'; % [ -1, % - cos(gpuls*t)*sin(phas) - sin(gpuls*t)*cos(phas), % amp*sin(gpuls*t)*sin(phas) - amp*cos(gpuls*t)*cos(phas)]; %jacobian for residuals^2 %J2(i,:)=[ 2*ofs - 2*ymes + 2*amp*cos(puls*t)*sin(phas) + 2*amp*sin(puls*t)*cos(phas), % 2*(cos(puls*t)*sin(phas) + sin(puls*t)*cos(phas))*(ofs - ymes + amp*cos(puls*t)*sin(phas) + amp*sin(puls*t)*cos(phas)), % 2*(amp*cos(puls*t)*cos(phas) - amp*sin(puls*t)*sin(phas))*(ofs - ymes + amp*cos(puls*t)*sin(phas) + amp*sin(puls*t)*cos(phas))]; end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [res] = displaySinNonLinear(tmin,tmax,x,style) global gpuls ofs=x(1); amp=x(2); phas=x(3); nla=x(4); nlb=x(5); nlc=x(6); t=tmin:0.1:tmax; reconsperfect=ofs+amp*sin(gpuls.*t+phas); recons=nla * reconsperfect.^2 + nlb * reconsperfect + nlc; plot(t,recons,style) end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [X covarianceOut]=fitSinusLinear(datax,datay,puls) %linear method for known pulsation %https://fr.mathworks.com/matlabcentral/fileexchange/41246-sine-function-fit global gnoiseLevel symbolicComputation=false nbdata=max(size(datax)); A=zeros(nbdata,3); B=zeros(nbdata,1); for i=1:nbdata t=datax(i); ymes=datay(i); B(i)=ymes; dx=puls*t; A(i,:)= [1 cos(dx) sin(dx)] ; end C=(A'*A)^(-1)*A'; %solve the system by expressing it as a linear product Xa=C*B; %propagate uncertainty from datay to Xa estimateVarianceFromMSE=true if ~estimateVarianceFromMSE varianceIn=gnoiseLevel^2 * eye(nbdata); else %in real case, the input variance should be estimated thanks to the MSE %varianceIn=zeros(nbdata); %for i=1:nbdata %t=datax(i); %ymes=datay(i); %dx=puls*t; %ypred=(Xa(1)*1+ Xa(2)* cos(dx) + Xa(3)* sin(dx)); %err=ymes- ypred; %varianceIn(i,i)=err^2; %end err=A*Xa-B; varianceIn=diag(err.*err); end %covariance for the internal parameterization covarianceOutIntern=C*varianceIn*C'; %check if there is covariance (diag matrix) covarianceOutIntern-diag([covarianceOutIntern(1,1), covarianceOutIntern(2,2), covarianceOutIntern(3,3)]); %this uncertainty has to be transfered to the final parameterization if symbolicComputation a=sym('a','real'); a=a; b1 = sym('b1','real'); b2 = sym('b2','real'); b=sqrt(b1*b1+b2*b2); %c=wrapTo2Pi(atan2(b1,b2)); %bring c between 0 and 2pi c=atan(b1/b2); %bring c between 0 and 2pi jacobian(b,[b1,b2]) % [ b1/(b1^2 + b2^2)^(1/2), b2/(b1^2 + b2^2)^(1/2)] jacobian(c,[b1,b2]) % [ 1/(b2*(b*1^2/b2^2 + 1)), -b1/(b2^2*(b1^2/b2^2 + 1))] jacobian([a,b,c],[a,b1,b2]) %[1, 0 , 0; %0, b1/(b1^2 + b2^2)^(1/2), b2/(b1^2 + b2^2)^(1/2); %0, 1/(b2*(b1^2/b2^2 + 1)), -b1/(b2^2*(b1^2/b2^2 + 1))] end a=Xa(1); b1=Xa(2); b2=Xa(3); %compute b & c b=sqrt(b1*b1+b2*b2); c=wrapTo2Pi(atan2(b1,b2)); %bring c between 0 and 2pi %compare c with %wt*ud JJ=[1, 0 , 0; 0, b1/(b1^2 + b2^2)^(1/2), b2/(b1^2 + b2^2)^(1/2); 0, 1/(b2*(b1^2/b2^2 + 1)), -b1/(b2^2*(b1^2/b2^2 + 1))] covarianceOut=JJ*covarianceOutIntern*JJ' covarianceOut-diag([covarianceOut(1,1), covarianceOut(2,2), covarianceOut(3,3)]); X=[a b c]; if symbolicComputation cdx1 = sym('cdx1','real'); sdx1 = sym('sdx1','real'); y1= sym('y1', 'real'); cdx2 = sym('cdx2','real'); sdx2 = sym('sdx2','real'); y2= sym('y2', 'real'); cdx3 = sym('cdx3','real'); sdx3 = sym('sdx3','real'); y3= sym('y3', 'real'); cdx4 = sym('cdx4','real'); sdx4 = sym('sdx4','real'); y4= sym('y4', 'real'); A=[1 cdx1 sdx1; 1 cdx2 sdx2; 1 cdx3 sdx3] B=[y1;y2;y3] solution=simplify((A'*A)^(-1)*A'*B) A=[1 cdx1 sdx1; 1 cdx2 sdx2; 1 cdx3 sdx3; 1 cdx4 sdx4] B=[y1;y2;y3;y4] C=simplify((A'*A)^(-1)*A') leastSquaresSolution=simplify(C*B) %practically, an incremental algorithm should keep track of the %symetric matrix %(A'*A)=[ 4, cdx1 + cdx2 + cdx3 + cdx4, sdx1 + sdx2 + sdx3 + sdx4] % [ cdx1 + cdx2 + cdx3 + cdx4, cdx1^2 + cdx2^2 + cdx3^2 + cdx4^2, cdx1*sdx1 + cdx2*sdx2 + cdx3*sdx3 + cdx4*sdx4] % [ sdx1 + sdx2 + sdx3 + sdx4, cdx1*sdx1 + cdx2*sdx2 + cdx3*sdx3 + cdx4*sdx4, sdx1^2 + sdx2^2 + sdx3^2 + sdx4^2] %and the vector %(A'*B)= [y1 + y2 + y3 + y4 % cdx1*y1 + cdx2*y2 + cdx3*y3 + cdx4*y4 % sdx1*y1 + sdx2*y2 + sdx3*y3 + sdx4*y4] var1 = sym('var1','real'); var2 = sym('var2','real'); var3 = sym('var3','real'); var4 = sym('var4','real'); %for constant known variance on input data varIn=diag([var1,var1,var1,var1]); simplify(A'*varIn*A) %[ 4*var1, var1*(cdx1 + cdx2 + cdx3 + cdx4), var1*(sdx1 + sdx2 + sdx3 + sdx4)] %[ var1*(cdx1 + cdx2 + cdx3 + cdx4), var1*(cdx1^2 + cdx2^2 + cdx3^2 + cdx4^2), var1*(cdx1*sdx1 + cdx2*sdx2 + cdx3*sdx3 + cdx4*sdx4)] %[ var1*(sdx1 + sdx2 + sdx3 + sdx4), var1*(cdx1*sdx1 + cdx2*sdx2 + cdx3*sdx3 + cdx4*sdx4), var1*(sdx1^2 + sdx2^2 + sdx3^2 + sdx4^2)] %for variances obtained from MSE varIn=diag([var1,var2,var3,var4]); simplify(A'*varIn*A) %[ var1 + var2 + var3 + var4, cdx1*var1 + cdx2*var2 + cdx3*var3 + cdx4*var4, sdx1*var1 + sdx2*var2 + sdx3*var3 + sdx4*var4] %[ cdx1*var1 + cdx2*var2 + cdx3*var3 + cdx4*var4, var1*cdx1^2 + var2*cdx2^2 + var3*cdx3^2 + var4*cdx4^2, cdx1*sdx1*var1 + cdx2*sdx2*var2 + cdx3*sdx3*var3 + cdx4*sdx4*var4] %[ sdx1*var1 + sdx2*var2 + sdx3*var3 + sdx4*var4, cdx1*sdx1*var1 + cdx2*sdx2*var2 + cdx3*sdx3*var3 + cdx4*sdx4*var4, var1*sdx1^2 + var2*sdx2^2 + var3*sdx3^2 + var4*sdx4^2] end end % A.X=B % A'.A.X=A'.B %p 31 of http://www.stat.columbia.edu/~fwood/Teaching/w4315/Fall2009/lecture_11 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function displayResult(res,covar,name) %display mean and 3Sigma values nbdata=max(size(res)); s=''; s=sprintf('%s :',name); for n=1:nbdata s=sprintf('%s %d +/- %d ,',s,res(n),3*sqrt(covar(n,n))); end disp(s); end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function test() %computation of the inverse of a symetric 3x3 matrix if false a1 = sym('ATAa1','real'); b1 = sym('ATAb1','real'); c1 = sym('ATAc1','real'); d1 = sym('ATAd1','real'); e1 = sym('ATAe1','real'); f1 = sym('ATAf1','real'); A1=[a1 b1 c1 ; b1 d1 e1; c1 e1 f1] % a2 = sym('a2','real'); % b2 = sym('b2','real'); % c2 = sym('c2','real'); % d2 = sym('d2','real'); % e2 = sym('e2','real'); % f2 = sym('f2','real'); % A2=[a2 b2 c2 ; b2 d2 e2; c2 e2 f2] % prod=A1*A2 % equations=reshape(prod-eye(3),9,1) % solve(equations(1:6),[a2 b2 c2 d2 e2 f2]) % solve(equations(1:6),a2 ) % http://www.tutorvista.com/content/math/inverse-of-symmetric-matrix/ % A-1= adj(A)/det(A) A2tmp=adjoint(A1) determinant=det(A1) A2=A2tmp/determinant end end
- fitSinusLinearOptimized.m
function [X covarianceOut, err]=fitSinusLinearOptimized(datax,datay,puls) nbdata=max(size(datax)); A=zeros(nbdata,3); B=zeros(nbdata,1); err=zeros(nbdata,1); var=zeros(nbdata,1); ATA=zeros(3,3); ATB=zeros(3,1); ATAa=0; ATAb=0; ATAc=0; ATAd=0; ATAe=0; ATAf=0; ATBa=0; ATBb=0; ATBc=0; cdx=zeros(nbdata,1); sdx=zeros(nbdata,1); cdx2=zeros(nbdata,1); sdx2=zeros(nbdata,1); cdxsdx=zeros(nbdata,1); for i=1:nbdata x=datax(i); y=datay(i); B(i)=y; dx=puls*x; cx=cos(dx); sx=sin(dx); cx2=cx*cx; sx2=sx*sx; cxsx=cx*sx; cdx(i)=cx; sdx(i)=sx; cdx2(i)=cx2; sdx2(i)=sx2; cdxsdx(i)=cxsx; ATAa=ATAa+1; ATAb=ATAb+cx; ATAc=ATAc+sx; ATAd=ATAd+cx2; ATAe=ATAe+cxsx; ATAf=ATAf+sx2; ATBa=ATBa+y; ATBb=ATBb+cx*y; ATBc=ATBc+sx*y; end %complete symetric matrices %ATA=[ATAa , ATAb , ATAc ; ATAb , ATAd , ATAe ; ATAc , ATAe , ATAf]; %ATB=[ATBa , ATBb , ATBc ]'; %leastSquaresSolution=inv(ATA)* ATB %a=leastSquaresSolution(1); %b1=leastSquaresSolution(2); %b2=leastSquaresSolution(3); determinant =- ATAf*ATAb^2 + 2*ATAb*ATAc*ATAe - ATAd*ATAc^2 - ATAa*ATAe^2 + ATAa*ATAd*ATAf; ATAinva= (ATAd*ATAf - ATAe^2 )/determinant; ATAinvb= (ATAc*ATAe - ATAb*ATAf )/determinant; ATAinvc= (ATAb*ATAe - ATAc*ATAd )/determinant; ATAinvd= (ATAa*ATAf - ATAc^2 )/determinant; ATAinve= (ATAb*ATAc - ATAa*ATAe )/determinant; ATAinvf= (ATAa*ATAd - ATAb^2 )/determinant; ATAinv=[ ATAinva ATAinvb ATAinvc; ATAinvb ATAinvd ATAinve; ATAinvc ATAinve ATAinvf]; a =ATAinva * ATBa + ATAinvb * ATBb + ATAinvc * ATBc; b1=ATAinvb * ATBa + ATAinvd * ATBb + ATAinve * ATBc; b2=ATAinvc * ATBa + ATAinve * ATBb + ATAinvf * ATBc; Xa=[a b1 b2] %compute b & c b=sqrt(b1*b1+b2*b2); c=wrapTo2Pi(atan2(b1,b2)); %bring c between 0 and 2pi X=[a b c ]; %compute MSE and variance.... ATVarAa=0; ATVarAb=0; ATVarAc=0; ATVarAd=0; ATVarAe=0; ATVarAf=0; for i=1:nbdata er= 1 * a + cdx(i,1) * b1 + sdx(i,1) * b2; vari= er*er; err(i)=er; var(i)=vari; ATVarAa= ATVarAa + vari; ATVarAb= ATVarAb + cdx(i,1) * vari; ATVarAc= ATVarAc + sdx(i,1) * vari; ATVarAd= ATVarAd + cdx2(i,1) * vari; ATVarAe= ATVarAe + cdx(i,1)*sdx(i,1) * vari; ATVarAf= ATVarAf + sdx2(i,1) * vari; end ATVarA=[ ATVarAa ATVarAb ATVarAc; ATVarAb ATVarAd ATVarAe; ATVarAc ATVarAe ATVarAf]; covarianceOutIntern=ATAinv'*ATVarA*ATAinv; JJ=[1, 0 , 0; 0, b1/(b1^2 + b2^2)^(1/2), b2/(b1^2 + b2^2)^(1/2); 0, 1/(b2*(b1^2/b2^2 + 1)), -b1/(b2^2*(b1^2/b2^2 + 1))]; covarianceOut=JJ*covarianceOutIntern*JJ'; end
deflectometry.txt · Dernière modification : 2021/02/19 20:20 de 127.0.0.1