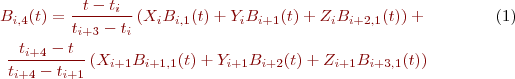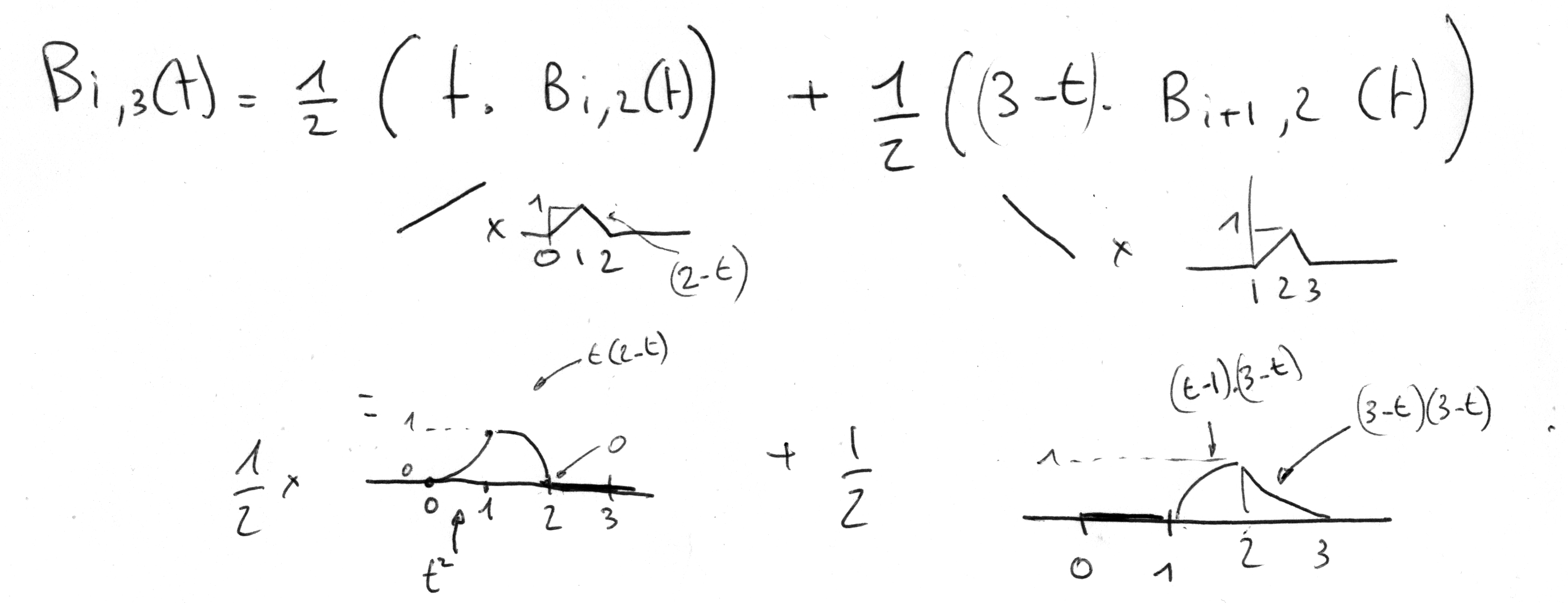WIKI de Bertrand VANDEPORTAELE

Outils pour utilisateurs

Outils du site

Piste : • nucs
Action disabled: diff
nucs

Ceci est une ancienne révision du document !

Table des matières

Développement des fonctions de Bases pour splines cubiques non uniformes NUCS

site avec demo: http://www.inf.ed.ac.uk/teaching/courses/cg/d3/nonbspline.html

cours: https://ocw.mit.edu/courses/mechanical-engineering/2-158j-computational-geometry-spring-2003/lecture-notes/lecnotes6.pdf

exercice: http://www.math.ucla.edu/~baker/pdf/pp_nonuniform.pdf

Papiers: https://theses.lib.vt.edu/theses/available/etd-100699-171723/unrestricted/chapter4.PDF

http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf

http://ftp.cs.wisc.edu/Approx/bsplbasic.pdf

http://www.maths.lse.ac.uk/Personal/jruf/papers/ruf_bspline.pdf

http://webee.technion.ac.il/Sites/People/YoninaEldar/Download/ME04c.pdf

https://fr.wikipedia.org/wiki/B-spline

$\mathbf{p}(t) = \sum_{i = 0}^{m} \mathbf{P}_{i} B_{i, k} (t) $

$B_{i, 1}(t) := \left\{ \begin{matrix} 1 & \mathrm{si} \quad t_i \leqslant t < t_{i + 1} \\ 0 & \mathrm{sinon} \end{matrix} \right. $

$B_{i, k}(t) := \frac{t - t_i}{t_{i+k-1} - t_i} B_{i, k - 1}(t) + \frac{t_{i + k} - t}{t_{i+k} - t_{i + 1}} B_{i + 1, k - 1}(t).$

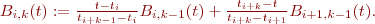
Implémentation Matlab

nucs.m
function  nucs(  )
%Non-uniform cubic B-splines  NON CUMULATIVES
%b. Vandeportaele
%d'après http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf
close all
clear all
 
%%%%IMPORTANT%%%%%%%%%
%pour spline linéaire
%k=2
%pour spline quadratique
%k=3
%pour spline cubique
k=4;% pour avoir 3 fonctions de base non nulles entre t=3 et t=4. Il s'agit de B0 à B3
%j'affiche les fonctions de base en surnombre, mais en fait il suffit de
%regarder les 4 fonctions de base sur l'intervale t=3 à t=4. et de
%substituer les indices pour les P et les t
for numerotest=1:2
    figure
    hold on
    axis equal
    if numerotest==1
        %pour distribution uniforme
        title('pour distribution uniforme');
        P0=2; t0=0;
        P1=3; t1=1;
        P2=4; t2=2;
        P3=5; t3=3;
        %more points
        P4=6; t4=4;
        P5=7; t5=5;
        P6=8; t6=6;
        P7=9; t7=7;
        P8=10; t8=8;
        P9=11; t9=9;
    else
        %pour distribution non uniforme
        title('pour distribution non uniforme');
        t1=1.1;
        t2=2.9;
    end
    %rangement dans des vecteurs
    listt=[t0;t1;t2;t3;t4;t5;t6;t7;t8;t9];
    listp=[P0;P1;P2;P3;P4;P5;P6;P7;P8;P9];
    %affichage des points de contrôle
    plot(listt, listp,'ko');
    Base=zeros(4,1);
    for t=0:0.01:9
        pt=0;
        %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
        %pour indices de 0 à +3: plus simple à comprendre mais ne gère pas
        %bien les 3 premiers points de la spline; ce sera la version à
        %implémenter lorsque l'on changera les indices au fûr et à mesure
        %for i=0:5
        %    Base(i +1) = B( i,k,t,listt);
        %    pt=pt+listp(i +1)*Base(i +1);
        %end
        %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
        %pour indices de -2 à +5: permet une visu correcte de la courbe
        %pour qu'elle passe par les points de contrôle
        %je suis obligé de ranger les fonctions de bases en décalé...
        %je n'affiche pas ces 2 fonctions de base B-2 et B-1 sur la figure
        %mais elles sont utilisées pour le calcul de pt
        if k==2
            indiceBaseMin=-1;
        elseif k==3
            indiceBaseMin=-2;  %ce n'est pas correct, il y a un offset... avec -1 aussi... ce n'est pas forcément grave car on s'intéresse aux splines cubiques
        else %k==4
            indiceBaseMin=-2;
        end
        for i=indiceBaseMin:5
            Base(-indiceBaseMin+ i +1) = B( i,k,t,listt);
            pt=pt+listp(-indiceBaseMin+ i +1)*Base(-indiceBaseMin+ i +1);
        end
        %Base
        %sum(Base)
        plot(t,Base(1),'gx');
        plot(t,Base(2),'bx');
        plot(t,Base(3),'kx');
        plot(t,Base(4),'mx');
        %affiche les fonctions de bases suivantes...
        plot(t,Base(5),'yx');
        plot(t,Base(6),'cx');
        %la courbe interpolée
        plot(t,pt,'r+');
    end
    legend('PI','B0','B1','B2','B3','B4','B5','p(t)');
    ylabel('p');
    xlabel('t');
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [ val ] = B( i,k,t,listt)
%for first index=1 because of matlab
if (i>=0)
    ti=listt(i           + 1);
else
    ti=listt(1);
end
 
 
if (i+1>=0)
    tip1=listt(i+1       + 1);
else
    tip1=listt(1);
end
if (i+k>=0)
    tipk=listt(i+k       + 1);
else
    tipk=listt(1);
end
if (i+k-1>=0)
    tipkm1=listt(i+k-1   + 1);
else
    tipkm1=listt(1);
end
if k==1
    if  (ti<= t) && (t<tip1)
        val =  1 ;
    else
        val = 0 ;
    end
    return;
else
    if (tipkm1 -ti) ~=0
        val1= ((t- ti) / (tipkm1 -ti)) * B( i,k-1,t,listt);
    else
        val1= 0;
    end
    if (tipk - tip1)~=0
        %version http://graphics.cs.cmu.edu/nsp/course/15-464/Fall05/papers/kimKimShin.pdf
        val2= ((tipk - t) / (tipk - tip1)) * B( i+1,k-1,t,listt);
        %version http://www.inf.ed.ac.uk/teaching/courses/cg/d3/nonbspline.html
        %il y a une erreur!
        %val2= ((tipk - t) / (tipkm1 - ti)) * B( i+1,k-1,t,listt);
        %autre version foireuse en (4.7 de https://theses.lib.vt.edu/theses/available/etd-100699-171723/unrestricted/chapter4.PDF)
        %val2= ((tip1 - t) / (tipk - tip1)) * B( i+1,k-1,t,listt);
    else
        val2= 0;
    end
    val=val1+val2;
    return;
end
end

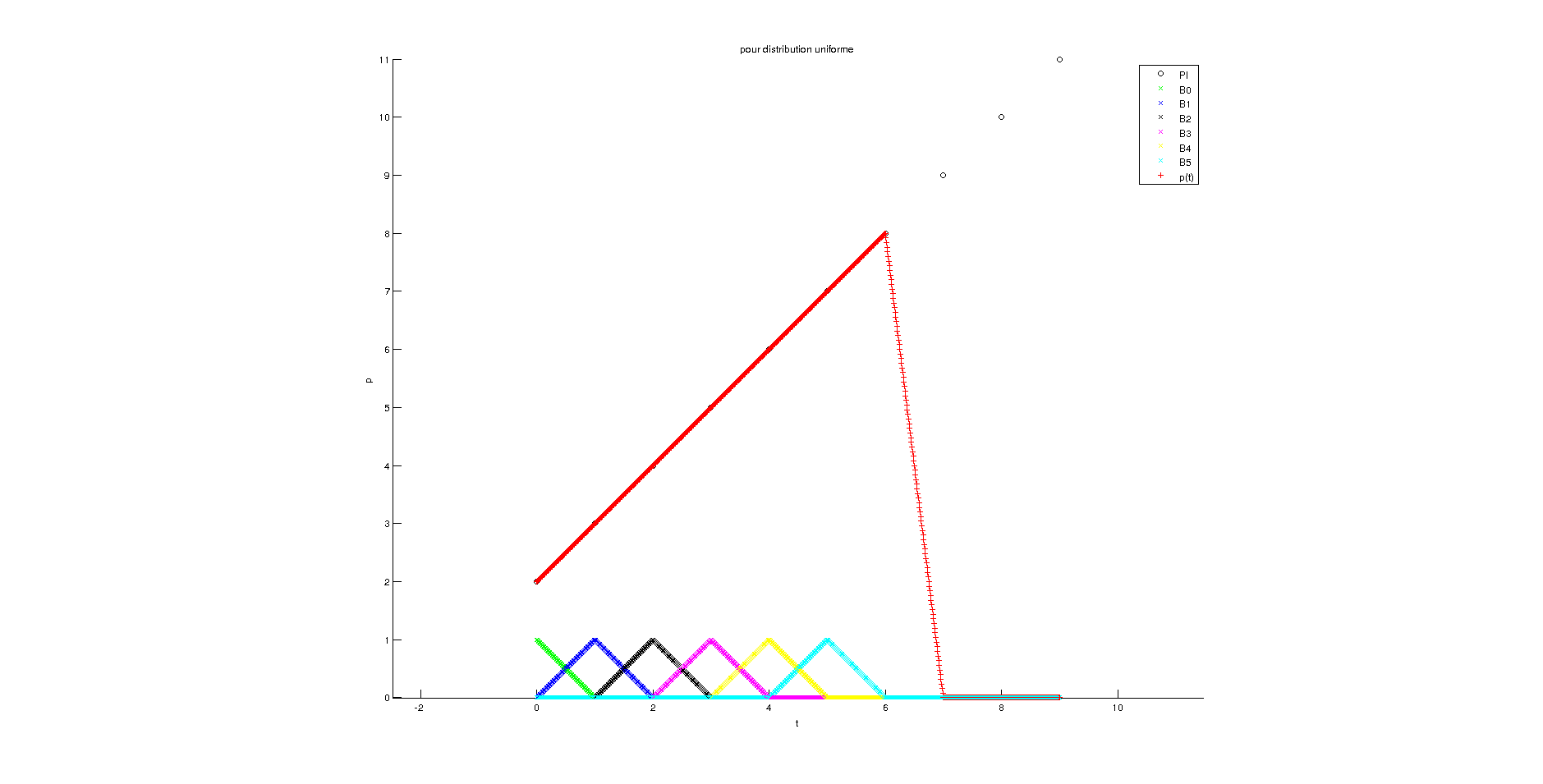
Résultat pour distribution uniforme et k=2

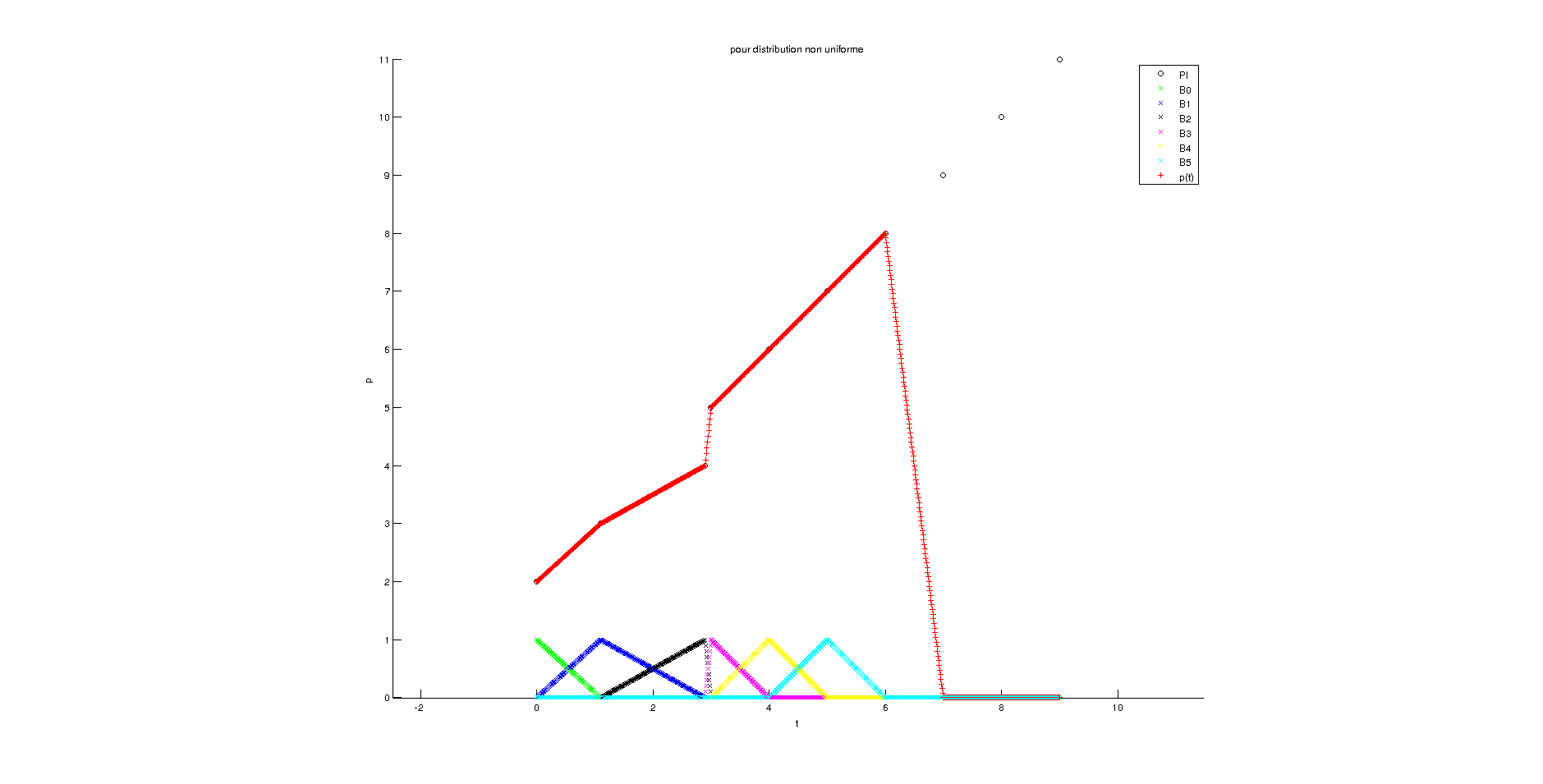
Résultat pour distribution non uniforme et k=2

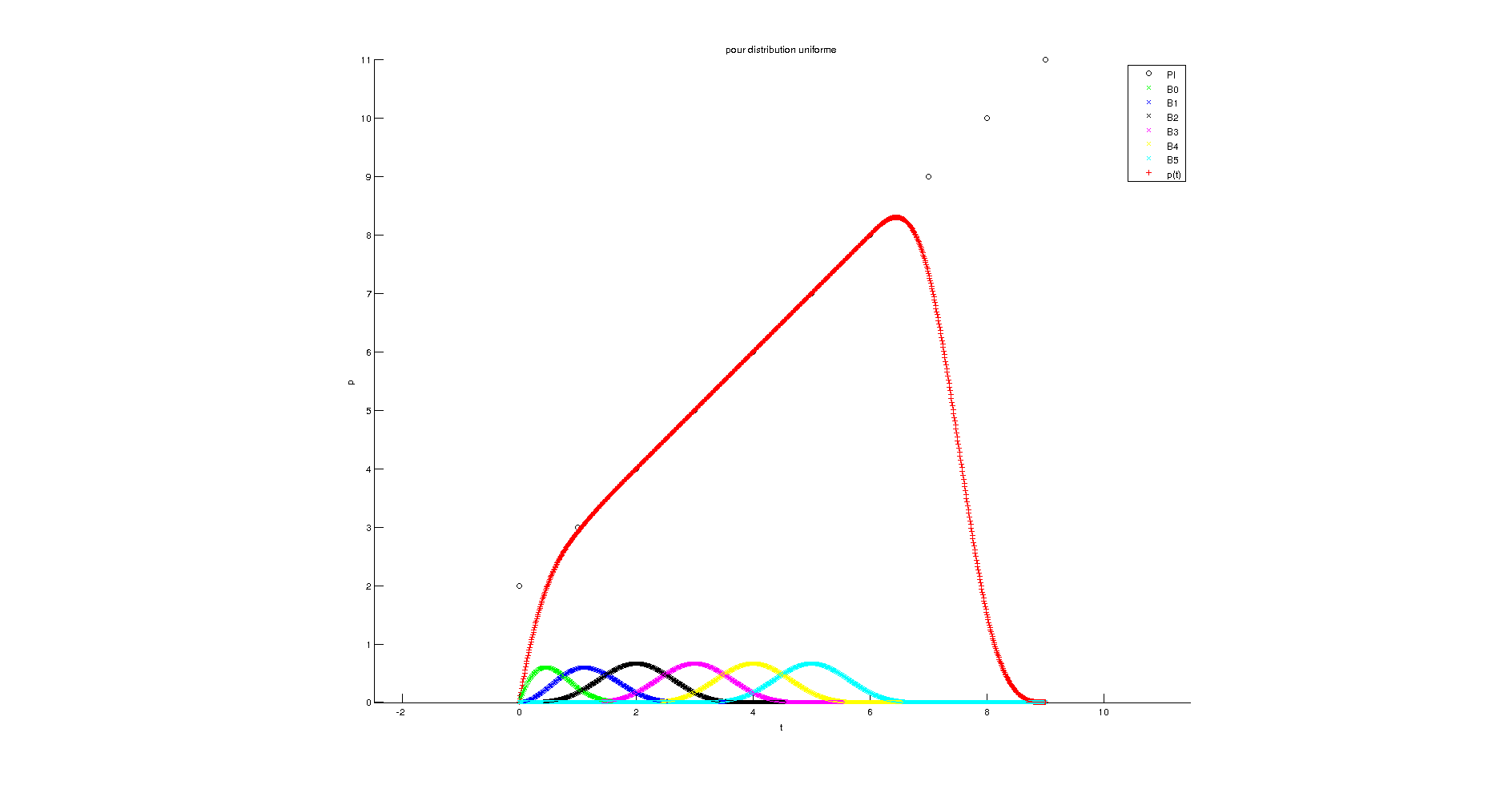
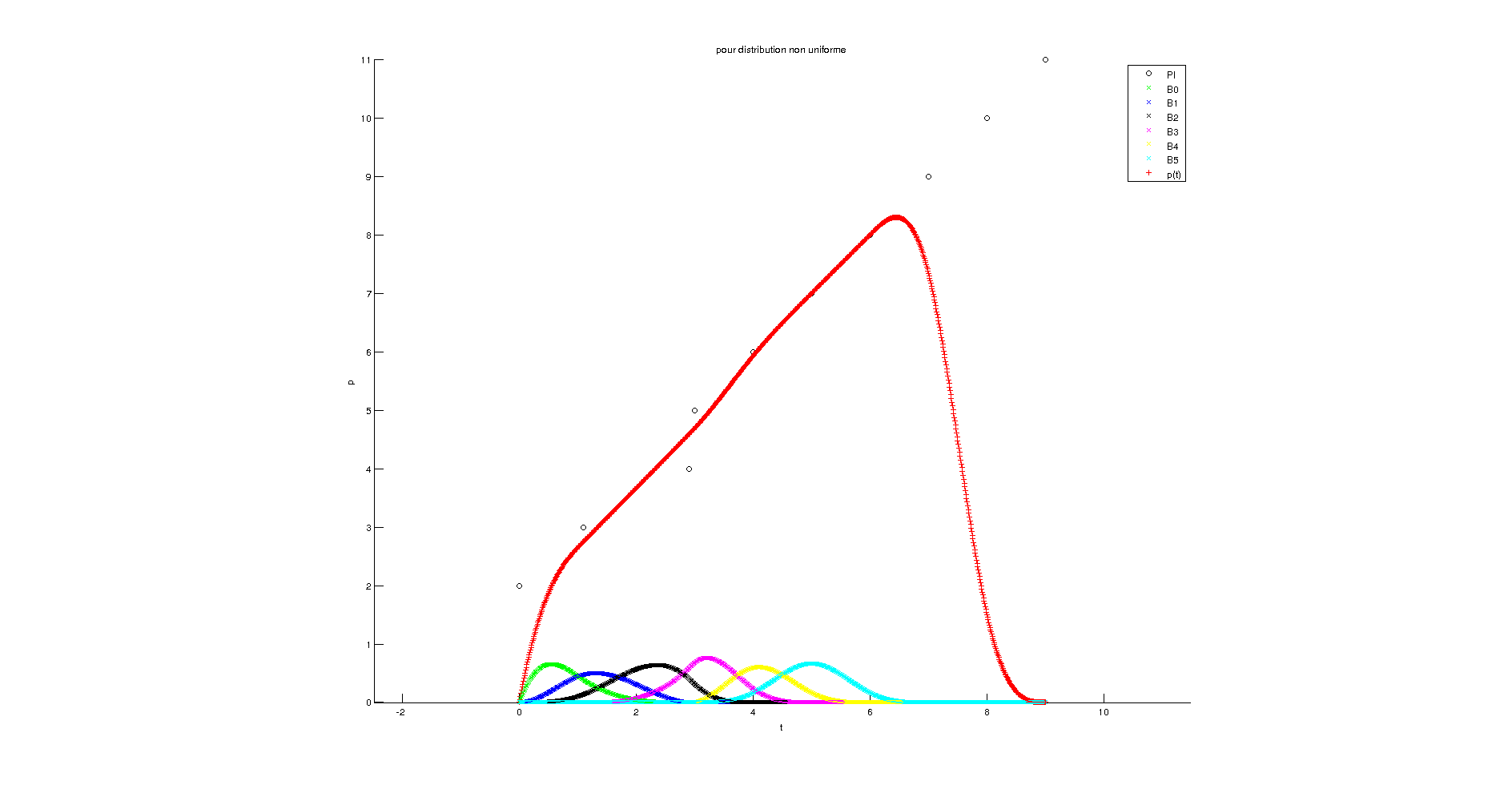
Résultat pour distribution uniforme et k=4

Résultat pour distribution non uniforme et k=4

Calcul des fonctions de base jusqu'à k=3 en considérant une distribution uniforme

Développement de l'équation de récurrence

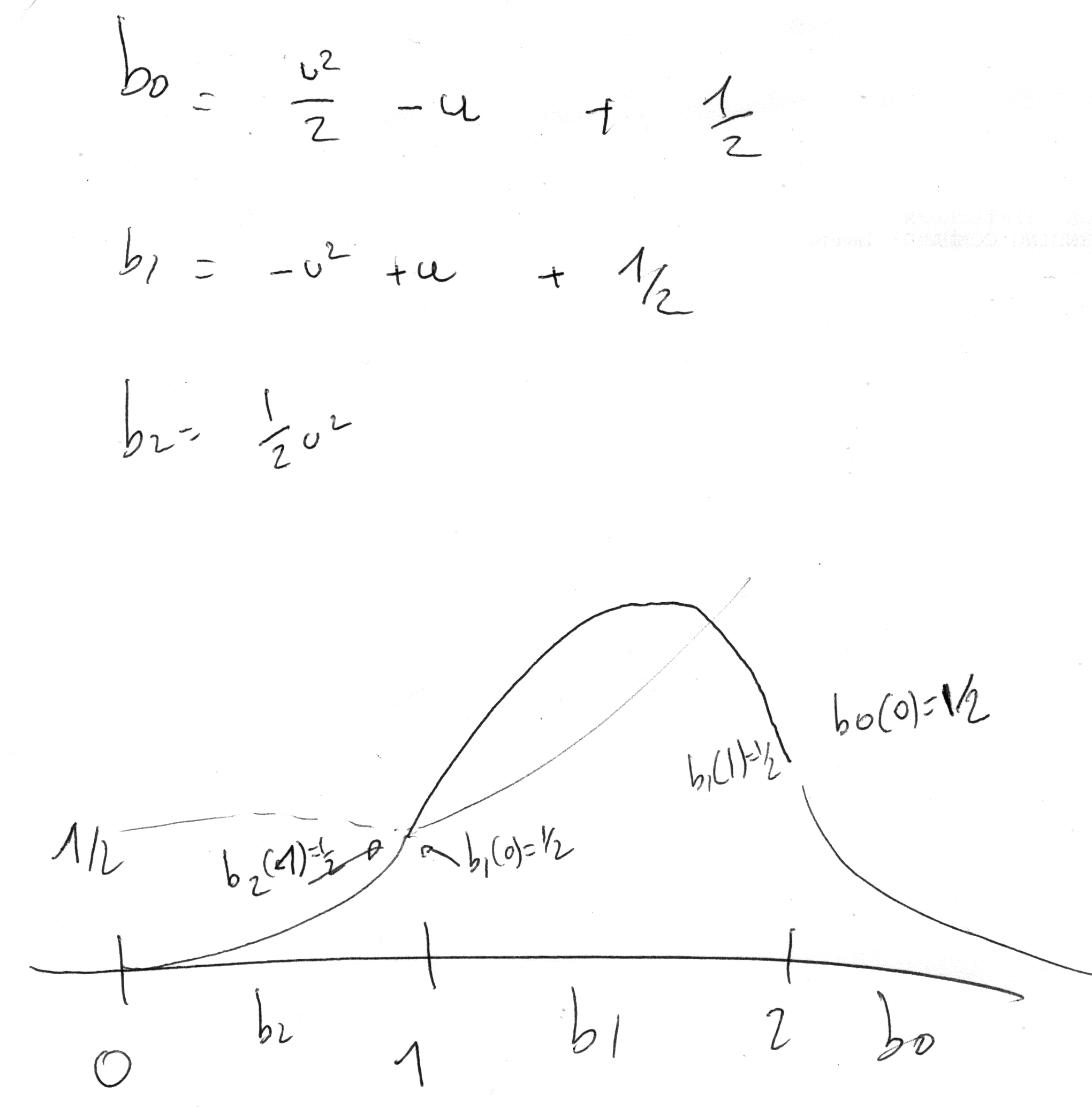
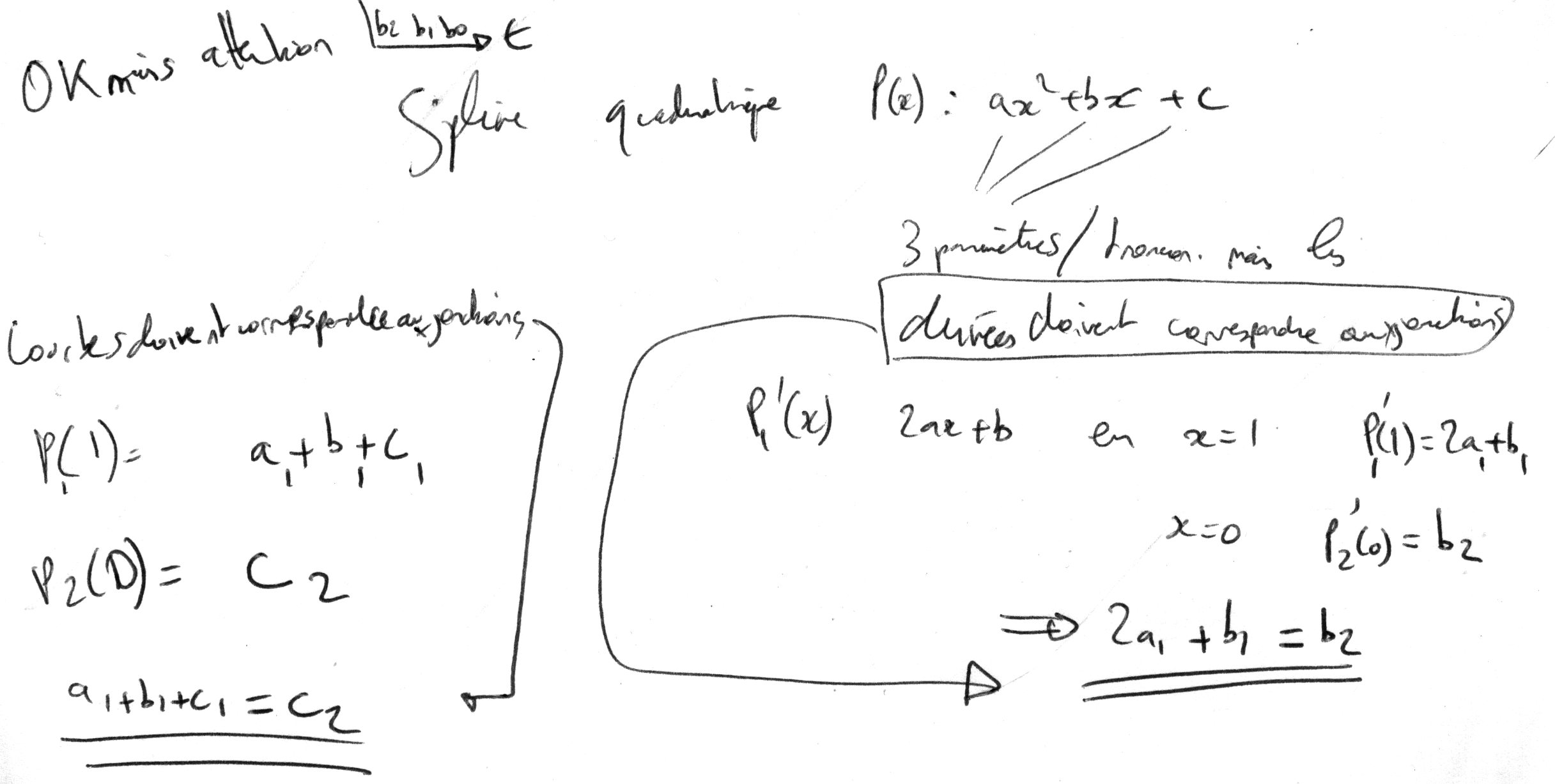
Dernière étape du développement de l'équation de récurrence pour splines quadratiques

etudebaseu_non_cumulatif.m
%B. Vandeportaele 2017
%étude du comportement des différentes fonctions de bases pour l'interpolation
close all
 
 
for ncurve=1:5
    figure
hold on
 
tb=[];
for u=0:0.01:1
%     b0=1;
%     b1=(u^3 -3*u^2 +3*u +5 )/6;
%     b2=(-2*u^3 +3*u^2 +3*u +1 )/6;
%     b3=(u^3 )/6;
%à partir du papier de Huixian, matrice M3 exprimée en colone
%spline de degré 3
if ncurve==1 
    b0=(-1*u^3 +3*u^2 -3*u +1 )/6;
    b1=(3*u^3 -6*u^2 +0*u +4 )/6;
    b2=(-3*u^3 +3*u^2 +3*u +1 )/6;
    b3=(u^3 )/6;
elseif ncurve==2
    b0=(-3*u^2 +6*u -3  )/6;
    b1=(9*u^2 -12*u +0 )/6;
    b2=(-9*u^2 +6*u +3 )/6;
    b3=(3*u^2 )/6;
elseif ncurve==3
    b0=(-6*u +6  )/6;
    b1=(18*u -12 )/6;
    b2=(-18*u +6 )/6;
    b3=(6*u )/6;
elseif ncurve==4
%     b0=(0.5 * u^2 );
%     b1=(-u^2 +3*u -3/2 );
%     b2=(0.5*u^2-3*u +9/2 );
%     b3=0;
%         
 
%Kaihuai M3 entre (8) et (9)
                               %   A     B    C
 b0=0.5*(1 - 2*u + 1  * u^2 ); %  1/2   -1    1/2
 b1=0.5*(1 + 2*u + -2 * u^2 ); %  -1     1    1/2
 b2=0.5*( u^2 );               %  1/2    0    0
    b3=0;
   elseif ncurve==5
       %dérivée du cas précédent 
 b0=0.5*(-2 + 2*u  );  
 b1=0.5*(2 - 4*u  ); 
 b2=0.5*(2* u );               
    b3=0;    
 
end
 
    tb=[tb;u,b0,b1,b2,b3,b0+b1+b2+b3];
end
 
plot (tb(:,1),tb(:,2),'r-');
plot (tb(:,1),tb(:,3),'g-');
plot (tb(:,1),tb(:,4),'b-');
plot (tb(:,1),tb(:,5),'k-');
 
plot (tb(:,1),tb(:,6),'c-');
%recolle les différentes fonctions de base pour illustrer le poids d'un
%Omega pour u^ évoluant de 0 à 4
plot (tb(:,1)+1*ones(size(tb(:,1))),tb(:,4),'b-');
plot (tb(:,1)+2*ones(size(tb(:,1))),tb(:,3),'g-');
plot (tb(:,1)+3*ones(size(tb(:,1))),tb(:,2),'r-');
 
legend('b0','b1','b2','b3','somme');
end
 
 
 
%retrouve l'expression polynomiale par morceau des Bi à partir de
%l'expression récurente
figure
hold on
axis equal
 
% 2*b2=u^2    => b2=1/2 . u^2
%b2 est défini entre 0 et 1 donc pas de changement
for u=0:0.01:1
    plot (u,(1/2)*u^2,'b+');
end
 
 
for u=1:0.01:2
    plot (u,(1/2)*u*(2-u),'r+');
end
for u=1:0.01:2
    plot (u,(1/2)*(u-1)*(3-u),'g+');
end
%2*b1 obtenu par somme de r+ et g+
%2*b1=  (u*(2-u))+((u-1)*(3-u)) = 2u -u^2 + 3u -u^2 -3 +u = -2u^2 +6u -3
%b1= -u^2 +3u-3/2
for u=1:0.01:2
    plot (u,(1/2)*((u*(2-u))+((u-1)*(3-u))),'y+');    
end
%ce b1 est défini entre 1 et 2 donc il faut faire un changement de variable
%u'=(u+1)
%b'1= -(u+1)^2       +3(u+1)-3/2
%      -u^2 -1 -2u   +3u  +3 -3/2
%      -u^2  +u  +1/2
%affiche b'1 entre 0 et 1
 for u=0:0.01:1
     plot (u,( -u^2  +u  +1/2),'yo');    
 end
 
 
%2*b0
%2*b0=(3-u)*(3-u)=9+u^2-6u
%b0= 1/2 u^2 -3u +9/2
for u=2:0.01:3
    plot (u,(1/2)*(3-u)*(3-u),'k+');
end
%ce b2 est défini entre 2 et 3 donc il faut faire un changement de variable
%u'=(u+2)
%b'2= 1/2 (u+2)^2           -3(u+2) +9/2
%   = 1/2 (u^2 + 4 + 4u)    -3u-6   +9/2
%   = 1/2 u^2 + 2 + 2u      -3u-6   +9/2
%   = 1/2 u^2 -1u +1/2
%affiche 2*b'2 entre 0 et 1
 for u=0:0.01:1
     plot (u,((1/2)*u^2  -u  +1/2),'ko');    
 end

NURBS

Attention les nurbs n'utilisent pas des fonctions de bases polynomiales mais des ratios…

extrait de https://fr.wikipedia.org/wiki/NURBS?veaction=edit

$\left\{\begin{array}{ll}N_{j}^0(t)= \left\{ \begin{array}{ll} 1 & si\; t_j \leq t < t_{j+1} \\ 0 & sinon \end{array} \right.\\ N_{j}^d(t)= \frac{t-t_j}{t_{j+d}-t_j} N_{j}^{d-1}(t)+\frac{t_{j+d+1}-t}{t_{j+d+1}-t_{j+1}}N_{j+1}^{d-1}(t)\end{array}\right.$

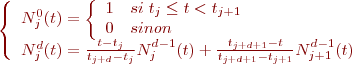
on s'intéresse à 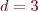$d=3$:

Développement:

$N_{j}^{d-1}(t)= \frac{t-t_j}{t_{j+{d-1}}-t_j} N_{j}^{{d-1}-1}(t)+\frac{t_{j+{d-1}+1}-t}{t_{j+{d-1}+1}-t_{j+1}}N_{j+1}^{{d-1}-1}(t) \\ = \frac{t-t_j}{t_{j+{d-1}}-t_j} N_{j}^{{d-2}}(t)+\frac{t_{j+{d}}-t}{t_{j+{d}}-t_{j+1}}N_{j+1}^{{d-2}}(t)$

$N_{{j+1}}^{d-1}(t)= \frac{t-t_{j+1}}{t_{{j+1}+{d-1}}-t_{j+1}} N_{{j+1}}^{{d-1}-1}(t)+\frac{t_{{j+1}+{d-1}+1}-t}{t_{{j+1}+{d-1}+1}-t_{{j+1}+1}}N_{{j+1}+1}^{{d-1}-1}(t) \\ = \frac{t-t_{j+1}}{t_{{j}+{d}}-t_{j+1}} N_{{j+1}}^{{d-2}}(t)+\frac{t_{{j}+{d}+1}-t}{t_{{j}+{d}+1}-t_{{j+2}}}N_{{j+2}}^{{d-2}}(t)$

$N_{j}^{d-2}(t)= \frac{t-t_j}{t_{j+{d-2}}-t_j} N_{j}^{{d-2}-1}(t)+\frac{t_{j+{d-2}+1}-t}{t_{j+{d-2}+1}-t_{j+1}}N_{j+1}^{{d-2}-1}(t) \\ = \frac{t-t_j}{t_{j+{d-2}}-t_j} N_{j}^{{d-3}}(t)+\frac{t_{j+{d-1}}-t}{t_{j+{d-1}}-t_{j+1}}N_{j+1}^{{d-3}}(t) $

$N_{{j+1}}^{d-2}(t)= \frac{t-t_{j+1}}{t_{{j+1}+{d-2}}-t_{j+1}} N_{{j+1}}^{{d-2}-1}(t)+\frac{t_{{j+1}+{d-2}+1}-t}{t_{{j+1}+{d-2}+1}-t_{{j+1}+1}}N_{{j+1}+1}^{{d-2}-1}(t) \\ = \frac{t-t_{j+1}}{t_{{j}+{d-1}}-t_{j+1}} N_{{j+1}}^{{d-3}}(t)+\frac{t_{{j}+{d}}-t}{t_{{j}+{d}}-t_{{j+2}}}N_{{j+2}}^{{d-3}}(t)$

$N_{{j+2}}^{d-2}(t)= \frac{t-t_{j+2}}{t_{{j+2}+{d-2}}-t_{j+2}} N_{{j+2}}^{{d-2}-1}(t)+\frac{t_{{j+2}+{d-2}+1}-t}{t_{{j+2}+{d-2}+1}-t_{{j+2}+1}}N_{{j+2}+1}^{{d-2}-1}(t) \\ = \frac{t-t_{j+2}}{t_{{j}+{d}}-t_{j+2}} N_{{j+2}}^{{d-3}}(t)+\frac{t_{{j}+{d}+1}-t}{t_{{j}+{d}+1}-t_{{j+3}}}N_{{j+3}}^{{d-3}}(t)$

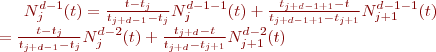
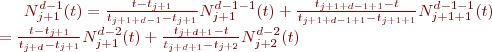
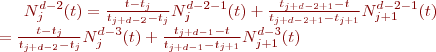
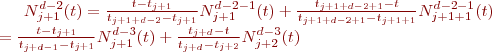
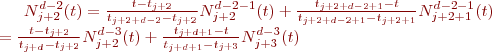
BSpline Non Uniforme

Développement des fonctions de base des BSpline non uniformes:

\begin{equation} B_{i,1}= \left\{ \begin{array}{l} 1 \quad \textrm{si} \quad t_i<t<t_{i+1} \\ 0 \quad \textrm{sinon} \end{array} \right. \end{equation}

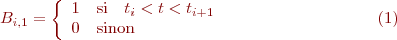
En utilisant cette définition, il est possible de calculer successivement les fonctions de base pour différents degrés en utilisant la formulation de récurrence de De Boor-Cox. Nous avons ainsi

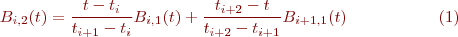
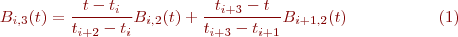
\begin{equation} \label{UnifBsplineBaseFuncDeg2} B_{i,2}(t) = \frac{t-t_i}{t_{i+1}-t_i} B_{i,1}(t) + \frac{t_{i+2}-t}{t_{i+2}-t_{i+1}}B_{i+1,1}(t) \end{equation}

\begin{equation} \label{UnifBsplineBaseFuncDeg3} B_{i,3}(t) = \frac{t-t_i}{t_{i+2}-t_i} B_{i,2}(t) + \frac{t_{i+3}-t}{t_{i+3}-t_{i+1}}B_{i+1,2}(t) \end{equation}

\begin{eqnarray} B_{i,3}(t) = \frac{t-t_i}{t_{i+2}-t_i} \left( \frac{t-t_i}{t_{i+1}-t_i} B_{i,1}(t) + \frac{t_{i+2}-t}{t_{i+2}-t_{i+1}}B_{i+1,1}(t) \right) +\\ \frac{t_{i+3}-t}{t_{i+3}-t_{i+1}} \left( \frac{t-t_{i+1}}{t_{i+2}-t_{i+1}} B_{i+1,1}(t) + \frac{t_{i+3}-t}{t_{i+3}-t_{i+2}}B_{i+2,1}(t) \right) \nonumber \end{eqnarray}

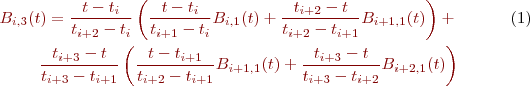
Après reformulation, on obtient:

\begin{eqnarray} \label{DeveloppedBaseDeg3} B_{i,3}(t) = \overbrace{\frac{(t-t_i)^2}{(t_{i+2}-t_i)(t_{i+1}-t_i)}}^{X_i}B_{i,1}(t) +\\ \overbrace{\left( \frac{(t-t_i)(t_{i+2}-t)}{(t_{i+2}-t_i)(t_{i+2}-t_{i+1})} + \frac{(t_{i+3}-t)(t-t_{i+1})}{(t_{i+3}-t_{i+1})(t_{i+2}-t_{i+1})}\right)}^{Y_i}B_{i+1,1}(t) + \nonumber \\ \overbrace{\frac{(t_{i+3}-t)^2}{(t_{i+3}-t_{i+1})(t_{i+3}-t_{i+2})}}^{Z_i}B_{i+2,1}(t) \nonumber \end{eqnarray}

\begin{equation} \label{UnifBsplineBaseFuncDeg4} B_{i,4}(t) = \frac{t-t_i}{t_{i+3}-t_i} B_{i,3}(t) + \frac{t_{i+4}-t}{t_{i+4}-t_{i+1}}B_{i+1,3}(t) \end{equation}

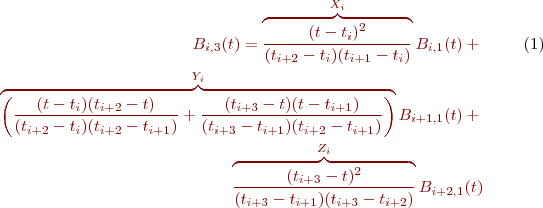
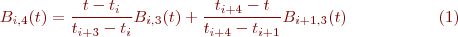
on peut développer la fonction de base pour k=4 tel que:

\begin{eqnarray} \label{UnifBsplineBaseFuncDeg4} B_{i,4}(t) = \frac{t-t_i}{t_{i+3}-t_i} \left(X_i B_{i,1}(t) + Y_i B_{i+1}(t) + Z_i B_{i+2,1}(t)\right) + \\ \frac{t_{i+4}-t}{t_{i+4}-t_{i+1}} \left(X_{i+1} B_{i+1,1}(t) + Y_{i+1} B_{i+2}(t) + Z_{i+1} B_{i+3,1}(t)\right) \nonumber \end{eqnarray}

nucs.1509442951.txt.gz · Dernière modification : 2017/10/31 10:42 de bvandepo